Despeje de Ecuaciones: Estrategias y Excepciones Clave

 

El  método de factorización de un TCP (Trinomio Cuadrado Perfecto) por adición y sustracción también es conocido como el método para completar cuadrados. Este método es muy parecido al trinomio cuadrado perfecto con algunas diferencias en su segundo término.

 

¿Cómo se factoriza un Trinomio Cuadrado Perfecto por adición y subtracción?

• Debemos verificar que tenemos un trinomio.

 

• El primer y segundo término deben tener una raíz cuadrada perfecta.

 

• En el segundo término es donde difiere este método con el del trinomio cuadrado perfecto, puesto que no se cumple que su valor sea igual al primer y tercer término multiplicados por 2.

 

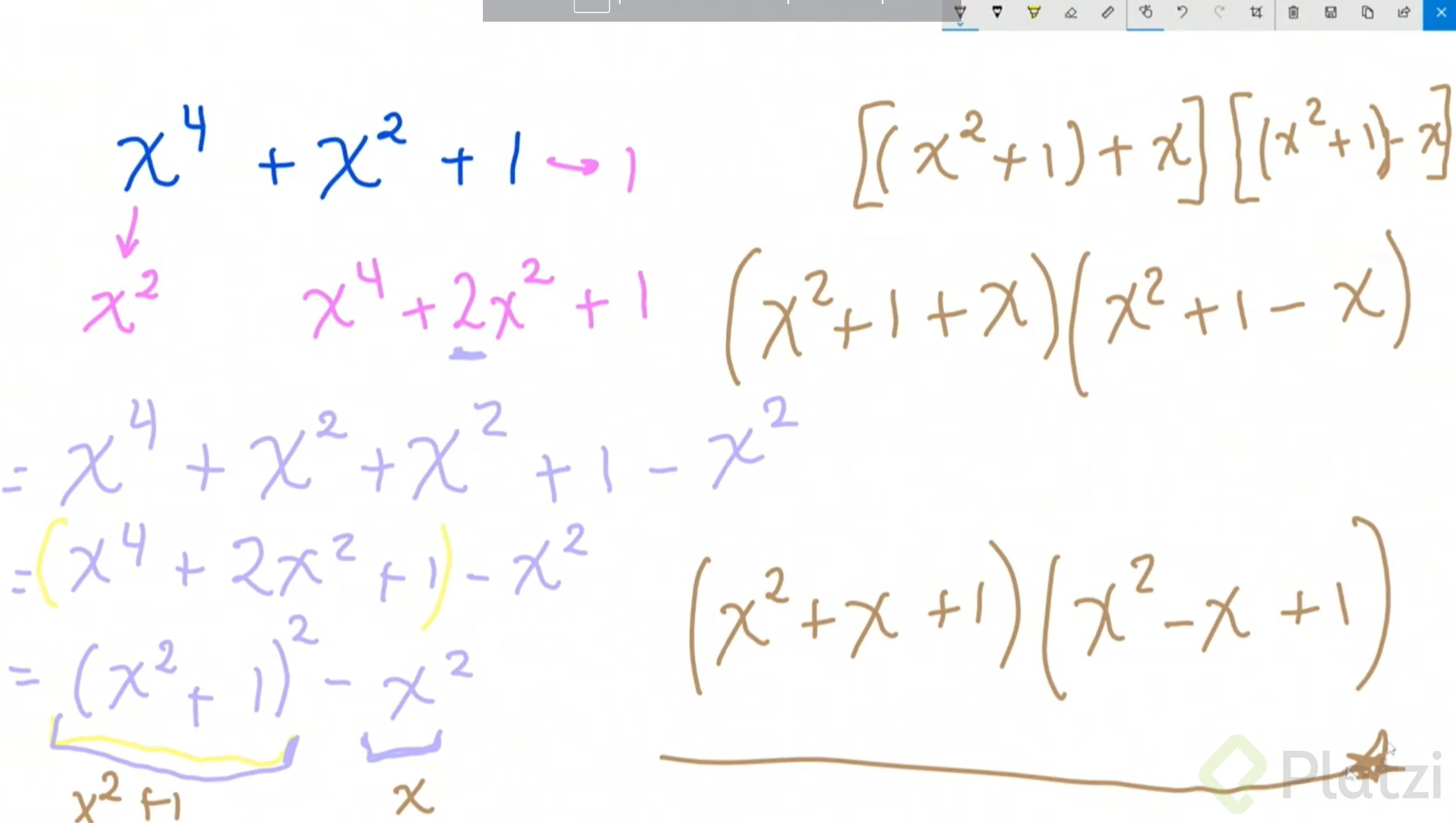
• Resolvemos el sistema como si fuera un trinomio cuadrado perfecto, y lo que nos haga falta para tener el segundo término completo (que cumpla las leyes del trinomio cuadrado perfecto) lo vamos a sumar y para no perder el equilibrio en el sistema, lo vamos a restar igualmente. Lo que ponemos lo tenemos que quitar.

 

• Factorizamos normalmente como un trinomio cuadrado perfecto, dejando por fuera del paréntesis resultante la parte que restamos en pasos anteriores al equilibrar el sistema.

 

• En muchos casos la expresión resultante será una diferencia de cuadrados perfectos, la cual podremos factorizar nuevamente.

 

• Es recomendable dejar el sistema siempre en su mínima expresión.