Domina la Regla de Cramer: Resuelve Sistemas de Ecuaciones con Determinantes Paso a Paso
Clase 19 de 21 • Curso de Álgebra y Funciones
Resumen
Las ecuaciones cuadráticas se dividen en completas e incompletas. Las ecuaciones completas son fácilmente resuelvas mediante la fórmula general. Las ecuaciones incompletas son muchos más fáciles de resolver y serán tratadas despues.
¿Qué es la fórmula general?
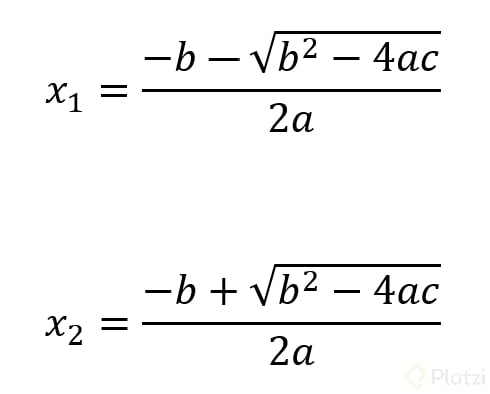
La fórmula general es la mejor herramienta para encontrar las raíces o soluciones a nuestras ecuaciones cuadráticas (de segundo grado).
Podemos resolver todas las ecuaciones cuadráticas usando la fórmula general o por medio de factorización con trinomios cuadrados.
La fórmula general es el resultado de despejar la x de nuestra ecuación base ax²+bx+ c.
Esta fórmula es conocida coloquialmente como “La chicharronera”