Factorización: Cuadrados y Cubos Simplificados

 

La diferencia de cuadrados se define como la resta del cuadrado del primer término menos el doble del producto de ambos términos, seguido por la suma del cuadrado del segundo término.

 

(x - y)^2 = x^2 - 2 * x * y + y^2

 

 

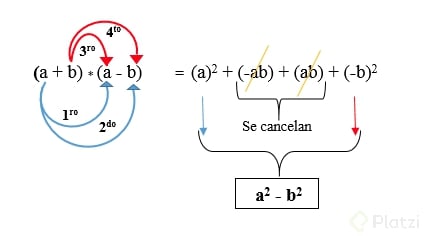
¿Cómo se factoriza una diferencia de cuadrados perfectos?

 

La factorización implica encontrar las raíces de los términos y colocarlas en un par de paréntesis. El orden de las raíces se mantiene como en la expresión original, y uno de los paréntesis lleva el signo más, mientras que el otro lleva el signo menos.

 

Ejemplo: (25x^2 y^4 - 121 = (5xy^2 + 11)(5xy^2 - 11))

 

Este proceso de factorización da lugar a lo que se llama binomios conjugados, donde “binomios” se refiere a los dos términos y “conjugados” alude al hecho de que uno tiene el signo positivo y el otro el negativo.

 

Ejemplos de diferencias de cuadrados

 

Aquí tienes algunos ejemplos de expresiones que pueden ser factorizadas utilizando la diferencia de cuadrados:

• (9a^4 - 16b^2)

 

• (x^6 - 64y^3)

Ejercicios resueltos de diferencias de cuadrados

 

A continuación, te presentamos ejercicios resueltos que te ayudarán a comprender y practicar la factorización de diferencias de cuadrados:

1. Factoriza (16x^4 - 81y^6)
   
   Solución: (16x^4 - 81y^6 = (4x^2 + 9y^3)(4x^2 - 9y^3))

 

1. Factoriza (49m^2 - 36n^2)
   
   Solución: (49m^2 - 36n^2 = (7m + 6n)(7m - 6n))

---

 

Cuando una expresión no cede debemos ir buscando métodos diferentes para resolverla

• Contrario de cuadrados perfectos son los binomios conjugados

 

• Los dos términos siempre son cuadrados

 

• Deberíamos encontrar las raíces cuadradas (exactas) de cada término y ponerlas en 2 paréntesis con + y - respectivamente