Propiedades algebraicas
Clase 5 de 21 • Curso de Álgebra y Funciones
Resumen
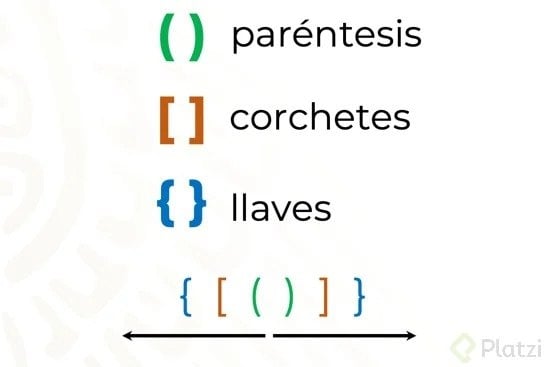
En el álgebra, los signos de agrupación desempeñan un papel crucial en la expresión y resolución de ecuaciones y problemas matemáticos. Estos signos, como los paréntesis (), corchetes [] y llaves {}, se utilizan para agrupar términos y establecer un orden de operaciones.
A continuación exploraremos los diferentes tipos de signos de agrupación algebraica, su correcto uso, ejemplos prácticos y consejos útiles para evitar errores comunes al usarlos.
¿Qué son los signos de agrupación algebraica?
Los signos de agrupación algebraica son símbolos que se emplean en las expresiones matemáticas para indicar cómo se deben realizar las operaciones y evaluar los términos dentro de un conjunto específico.
Estos signos permiten establecer el orden adecuado al resolver las operaciones y evitan ambigüedades en los cálculos.
¿Cómo se emplean correctamente los signos de agrupación?
Al utilizar los signos de agrupación en álgebra, es importante seguir algunas reglas básicas:
- Los paréntesis tienen la mayor prioridad y se resuelven primero.
- Si hay varios conjuntos de paréntesis, corchetes o llaves se evalúan de adentro hacia afuera.
- Los corchetes se usan principalmente para indicar multiplicación.
- Las llaves se emplean para agrupar conjuntos o establecer relaciones de pertenencia.
Tipos de signos de agrupación algebraica
Actualmente, podemos encontrar 3 tipos de signos de agrupación: paréntesis, corchetes y llaves.
1. Uso de los paréntesis
Los paréntesis se emplean para indicar que las operaciones dentro de ellos deben hacerse primero. Además, se emplean para agrupar términos que deben considerarse como una única entidad en una expresión algebraica.
Por ejemplo, en la expresión (2 + 3) * 4, se hace primero la operación dentro de los paréntesis antes de multiplicar el resultado por 4.
2. Uso de los corchetes
Los corchetes se utilizan en álgebra para indicar multiplicación. Por ejemplo, si tenemos la expresión 3[2 + (4 - 1)], primero se procede con la operación dentro de los paréntesis y luego se multiplica el resultado por 3.
3. Uso de las llaves
Las llaves se emplean en álgebra para indicar una relación de pertenencia o para agrupar conjuntos de términos. Por ejemplo, en la expresión {x ∈ N | x > 0}, las llaves se usan para representar el conjunto de números naturales mayores que cero.
Importancia de los signos de agrupación en álgebra
Los signos de agrupación son fundamentales en álgebra, ya que permiten establecer un orden adecuado de las operaciones y evitar ambigüedades en los cálculos. Al usar correctamente los signos de agrupación, se asegura una evaluación precisa de las expresiones y se obtienen resultados correctos.
Ejemplos de uso de los signos de agrupación en álgebra
Para ilustrar el uso de los signos de agrupación en álgebra, consideremos el siguiente ejemplo:
Expresión: 2 * (3 + 4) - 5
Primero, evaluamos la operación dentro de los paréntesis: 3 + 4 = 7. Luego, multiplicamos el resultado por 2: 2 * 7 = 14. Finalmente, restamos 5: 14 - 5 = 9.
Errores comunes al utilizar los signos de agrupación en álgebra
Al emplear los signos de agrupación en álgebra, es común cometer algunos errores. Algunos de los errores más comunes incluyen:
- Olvidar cerrar los paréntesis, corchetes o llaves.
- No seguir el orden adecuado de las operaciones.
- Realizar operaciones dentro de los signos de agrupación sin considerar su prioridad.