Cuantización de números en modelos de Machine Learning

La cuantización es un concepto crucial en Machine Learning, particularmente cuando se busca optimizar modelos de inteligencia artificial reduciendo los recursos de memoria necesarios. Para implementarlo efectivamente, es vital comprender cómo se almacena y procesa la información en las computadoras actuales.

¿Qué es exactamente la cuantización?

La cuantización busca reducir la cantidad de memoria necesaria para ejecutar modelos de Machine Learning, como los LLM (Large Language Models), disminuyendo la precisión en la representación numérica. Esto se logra convirtiendo números en coma flotante (que requieren más memoria) en números enteros (que usan menos memoria).

Imaginemos el modelo LAMA 3.1, que utiliza ocho billones de parámetros con una precisión de 16 bits; ocupa cerca de 16 GB de memoria. La cuantización permite almacenar estos mismos parámetros utilizando menos memoria.

¿Cómo se representan los datos en una computadora?

La información digital se almacena en bits (unos y ceros). La precisión determina cuántos valores diferentes podemos representar con esos bits. Por ejemplo:

• Con 3 bits podemos representar 8 números distintos (del 0 al 7).
• Con 8 bits (byte) podemos almacenar más valores.
• La mayoría de las computadoras actuales usan precisiones estándar de 8 (byte), 16 (chor), 32 (int) y 64 bits (long).

Además, las máquinas representan números negativos usando el "complemento a dos". El primer bit indica el signo del número: cero positivo, uno negativo.

¿Qué diferencia hay entre números enteros y números de coma flotante?

Para representar números con decimales, las computadoras utilizan el estándar IEEE 754. Este especifica un sistema formado por:

• Un bit de signo (positivo o negativo).
• Bits para un exponente.
• Bits para una fracción o mantisa.

Sumando estos bits obtenemos la precisión del número de coma flotante total, comúnmente 32 bits.

¿Cómo funciona la cuantización?

La cuantización transforma valores de coma flotante en números enteros y viceversa. Existen principalmente dos tipos de cuantización:

Cuantización asimétrica

Esta utiliza un rango de 0 hasta 255 (para una precisión de 8 bits). Se necesita calcular: - Alfa (valor máximo). - Beta (valor mínimo).

Luego se aplica una fórmula específica que reduce estos valores a números enteros dentro del rango.

Cuantización simétrica

Se basa exclusivamente en alfa, el mayor valor absoluto. Aquí, rango oscila típicamente entre -127 y 127, con el cero exactamente en medio.

Métodos para seleccionar parámetros en la cuantización

Los parámetros alfa y beta pueden seleccionarse usando diversas técnicas que influyen considerablemente en el rendimiento final del modelo cuantizado:

• Percentiles: Reducción del impacto de datos atípicos (outliers).
• MSE (mean square error): Minimiza errores a través de fuerza bruta (grid search).
• Cross Entropy: Importante especialmente en LLMs, optimizando para mantener intactas las distribuciones de probabilidad.

Quantization Aware Training (QAT), una técnica avanzada

Es un método innovador propuesto por Google DeepMind. En QAT, durante el entrenamiento se simula la cuantización, ayudando al modelo a reducir el error progresivamente. Esto permite que, al culminar el entrenamiento y cuantizar finalmente el modelo, la precisión general permanezca estable.

Utiliza un algoritmo llamado straight-through estimator (STE) para manejar el hecho de que la cuantización es una operación no derivable, permitiendo la derivación necesaria para la técnica de back propagation.

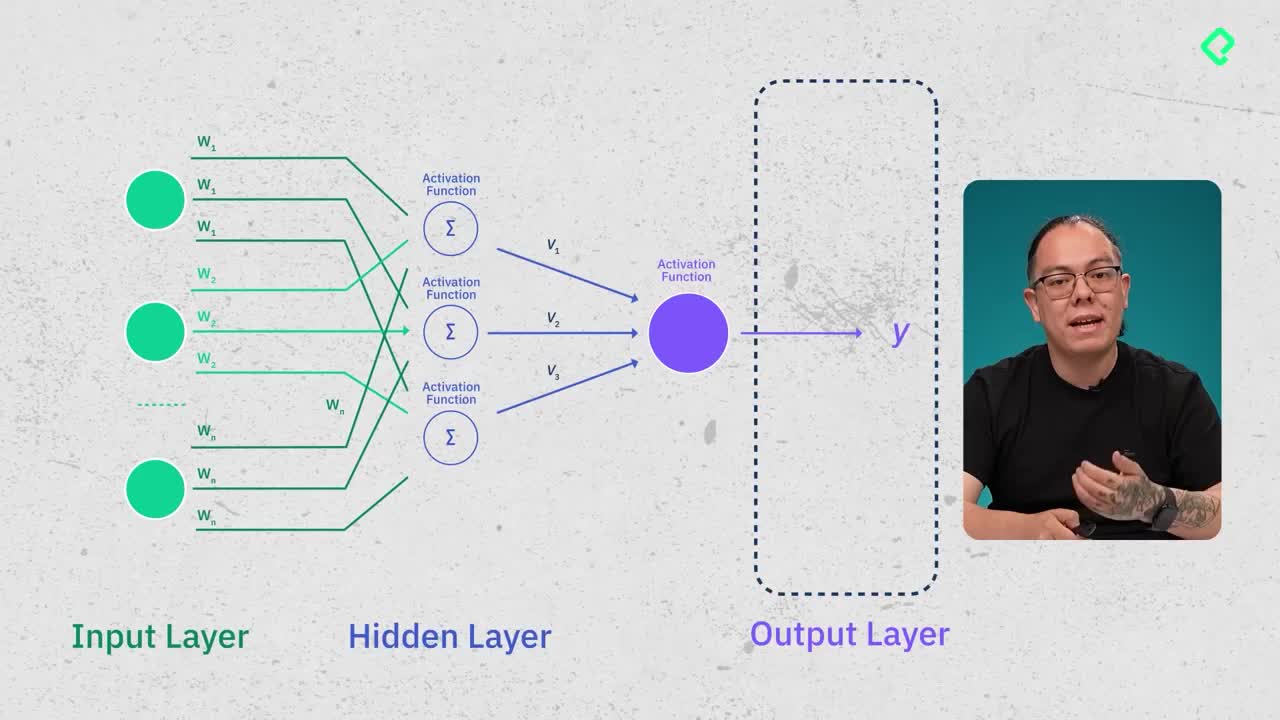
¿Qué debes cuantizar en una red neuronal?

En redes neuronales comunes como el perceptrón multicapa, cuantizamos: - Matriz de pesos (W). - Bias (b).

Las matrices de entrada (X) se cuantizan "sobre la marcha" (on the fly quantization), ya que sus valores cambian en cada consulta del usuario. Sin embargo, la matriz salida (Y) presenta desafíos adicionales y requiere métodos especializados.

La cuantización, bien implementada, permite usar modelos grandes y complejos en hardware más limitado, lo cual tiene enorme importancia práctica.