Conjuntos
Clase 10 de 15 • Curso de Lenguaje y Notación Matemática
Resumen
La teoría de conjuntos es una rama de las matemáticas y de la lógica que estudia a unos objetos llamados conjuntos que se encuentran conformados por elementos.
Esta teoría tiene por finalidad el estudio de las características de los conjuntos y las operaciones que pueden realizarse entre ellos.
Conjuntos
Es la colección de elementos considerada en sí misma como un objeto.
Ejemplos de conjuntos:
- Conjunto de las vocales: V = {a, e, i, o, u}
- Conjunto de los días de la semana: D = {domingo, lunes, martes, miércoles, jueves, viernes, sábado}
Operaciones de conjuntos
La teoría de conjuntos estudia una variedad de operaciones que se pueden efectuar entre estos. A continuación estudiaremos algunas de estas operaciones.
Unión de conjuntos
La unión de conjuntos consiste en la identificación de los elementos que pertenecen a varios conjuntos.
A ∪ B = {x | x ∈ A ∨ x ∈ B} (conjunto de todos los elementos que pertenecen a A o pertenecen a B).
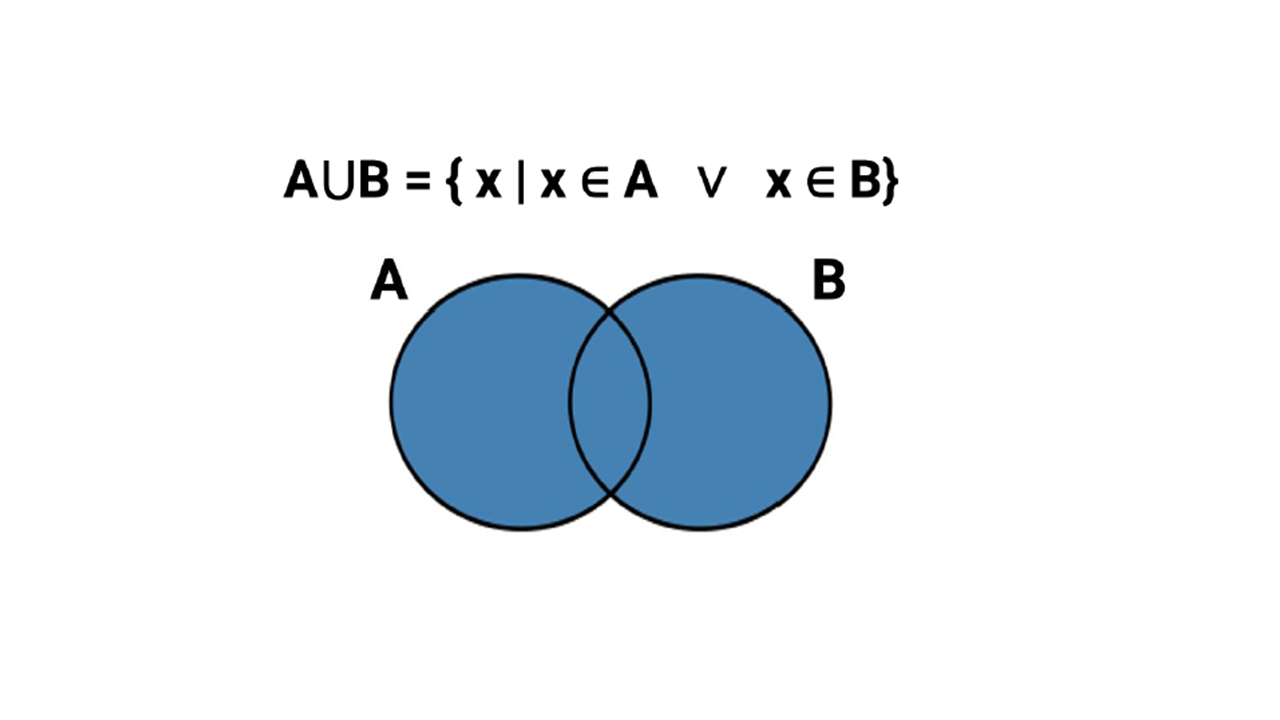
Es decir, sencillamente lo que expresa la unión de conjuntos es identificar todos los elementos que pertenecen a ambos conjuntos A o B.
Intersección de conjuntos
La intersección de conjuntos se define como la operación que resulta en un conjunto que contiene los elementos comunes o repetidos de otros conjuntos.
A ∩ B = {x | x ∈ A ∧ x ∈ B} (conjunto de todos los elementos que pertenecen a A y pertenecen a B).
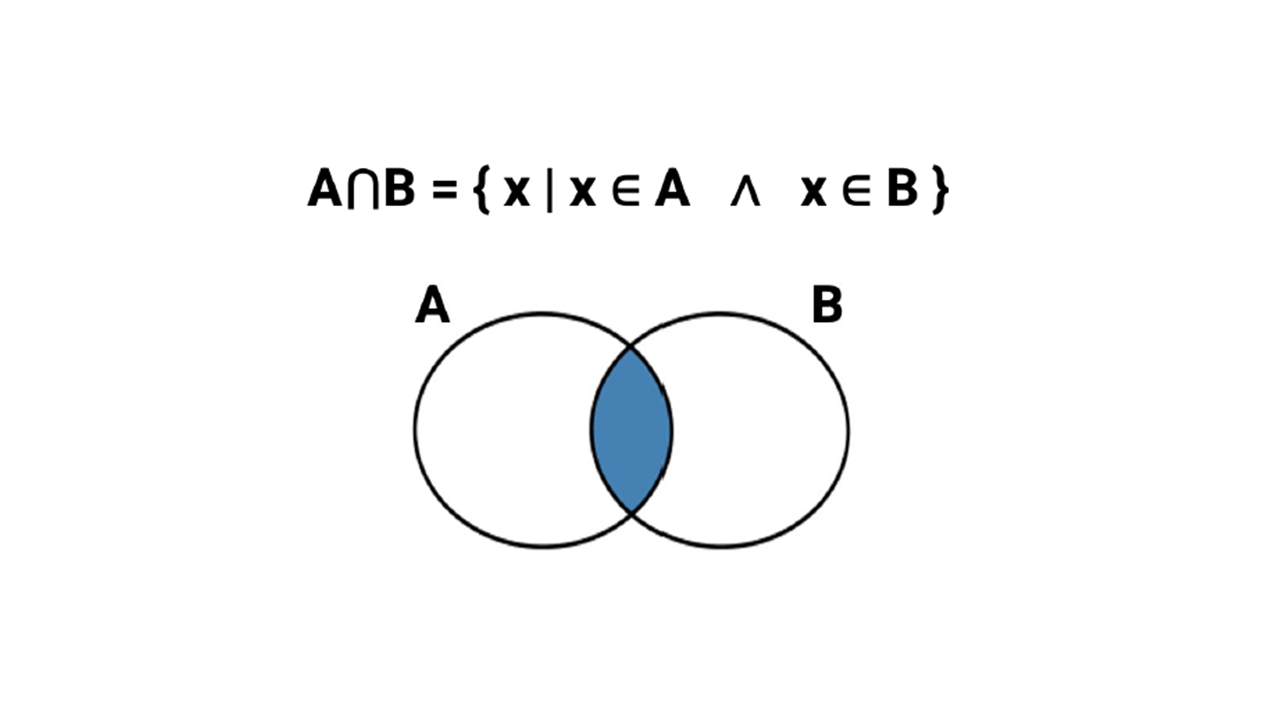
Diferencia de conjuntos
La diferencia de dos conjuntos es una operación que da como resultado otro conjunto con los elementos del primer conjunto sin los elementos del segundo conjunto.
A - B = {x | x ∈ A ∧ x ∉ B} (conjunto de todos los elementos que pertenecen a A, pero no pertenecen a B).
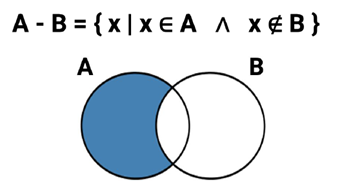
En la diferencia de conjuntos tenemos que esta se define por x tal que x pertenece al conjunto A, pero que no pertenecen al conjunto B. Es decir, significa que al conjunto A se le excluyen todos los elementos que pertenecen al conjunto B.
Es importante advertir que A-B ≠ B-A
Diferencia simétrica de conjuntos
La diferencia simétrica es el conjunto de todos los elementos que pertenecen a A, pero no pertenecen a B, o pertenecen a B, pero no pertenecen a A.
$A \triangle B = {x | x \in A-B \lor x \in B-A} = (A-B) \cup (B-A)$
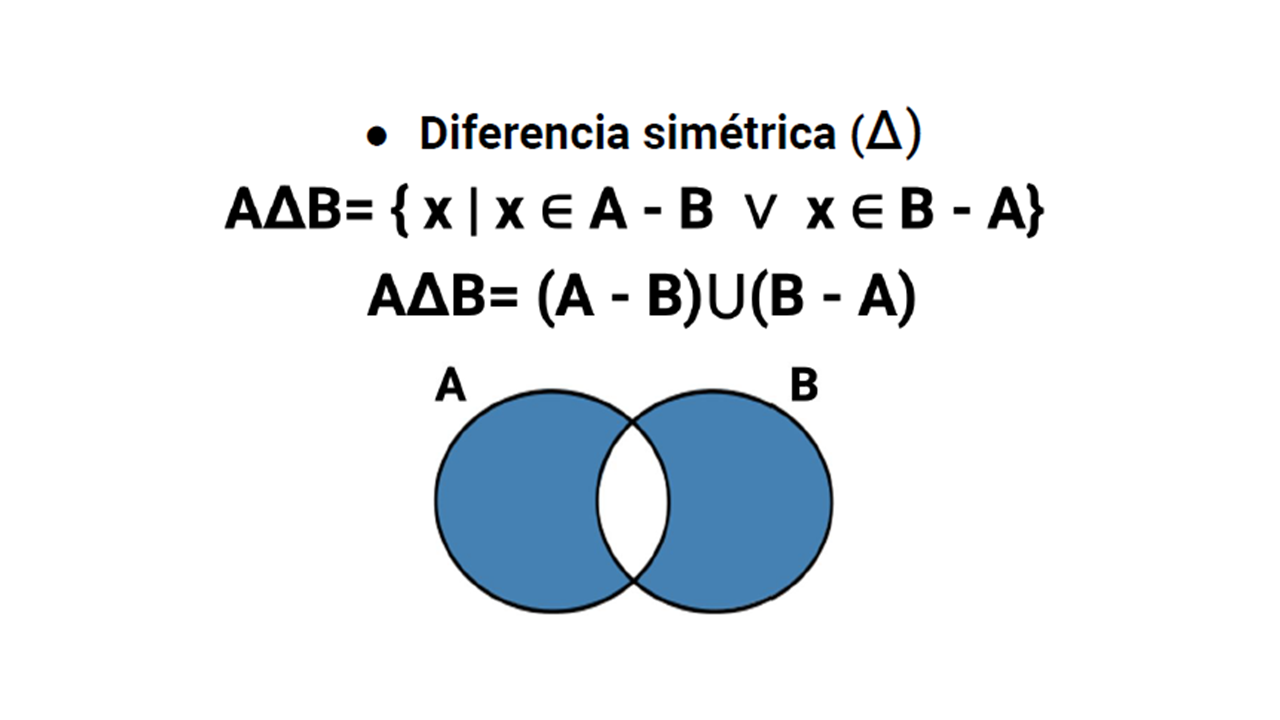
Por ejemplo, tenemos los conjuntos P y Q:
P = {a, e, i, o, u}
Q = {a, b, c, d, e}
Entonces,
PΔQ = {i, o, u, b, c, d}
Es decir, se excluyen los elementos comunes.
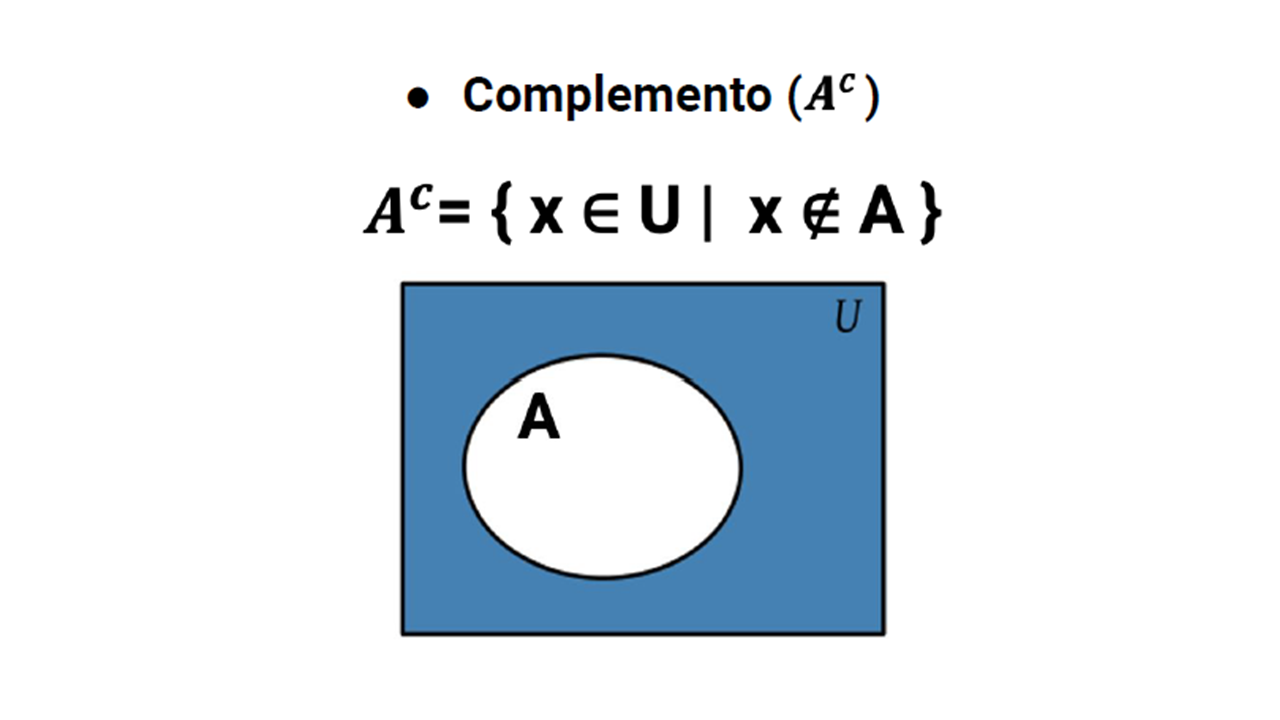
Complemento de conjuntos
El complemento del conjunto A es el conjunto formado por los elementos que pertenecen al conjunto universal (U), pero no pertenecen al conjunto $A.
Aᶜ = {x | x ∉ A ∧ x ∈ U}
Ejemplo:
Tenemos los conjuntos U, A y B.
U = {1, 2, 3, 4, 5, 6, 7, 8, 9}
A = {5, 6, 7, 8, 9}
B = {1, 6, 7, 8}
Entonces,
Aᶜ = {1, 2, 3, 4}
Bᶜ = {2, 3, 4, 5, 9}
A-B = {5, 9}
B-A = {1}
A Δ B = {1, 5, 9}
Contribución creada por: Néstor Arellano y Avilio Muñoz Vilchez.