Durante todo el módulo anterior interiorizamos en la carga de los datos, su exploración y limpieza y culminamos en la creación de un modelo mínimamente funcional. Durante esta y las siguientes sesiones interiorizaremos en el concepto de optimización del modelo para incrementar exponencialmente el rendimiento.

Durante esta sección comprenderemos qué es el overfitting y el underfitting, las mejores prácticas para ajustar los hiperparámetros de la red, métricas de monitoreo (como callbacks u early stopping) y a manejar el autotunner que Keras que actualizará los valores de diferentes parámetros según una serie de reglas establecidas.

¿Qué son los regularizadores?

La principal fuente de optimización de un modelo de deep learning se da mediante los regularizadores, técnicas que se usan para mejorar matemáticamente la convergencia de los datos y evitar atascamientos como el overfitting y el underfitting. Hablaremos de los 2 regularizadores más importantes: Dropout y Regularizadores L1 y L2.

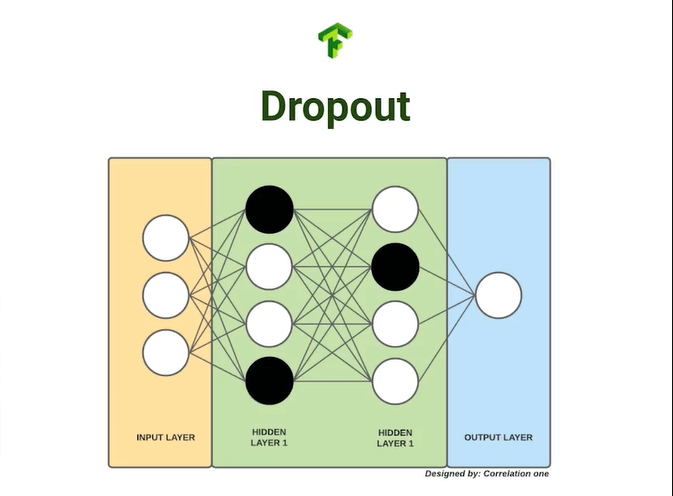
Dropout

El primer método es el dropout, una técnica que apaga un porcentaje aleatorio de neuronas por cada iteración obligando a aquellas activas a comprender un patrón general en vez de memorizar la estructura de los datos.

Regularizadores L1 y L2

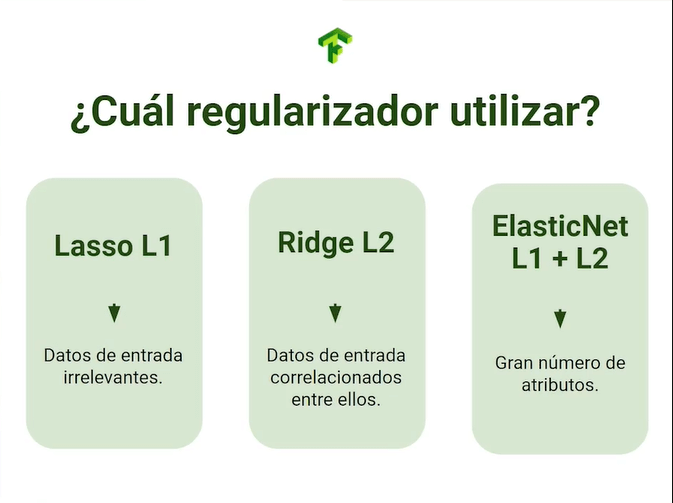
Los regularizadores son modificadores a las matrices de pesos que permiten ajustar sus valores y penalizan aquellos datos matemáticamente extremos, existen 2 tipos de regularizadores (L1 y L2) y una tercera variante que los combina ambos.

El regularizador Lasso L1 se usa cuando sospechas que pueden haber datos de entrada irrelevantes en tu red, su uso reducirá la cantidad de features innecesarias haciendo tu modelo más puro.

El regularizador Ridge L2 se usa cuando los datos de entrada se encuentran altamente correlacionados entre ellos, lo que aumentará la desviación. Su uso reducirá uniformemente la magnitud de los features armonizando el crecimiento de la red.

La combinación de los 2 regularizadores desemboca en ElasticNet, que será de alta utilidad en el manejo de modelos complejos con altas cantidades de features.

Con la teoría comprendida, vamos a mejorar nuestro modelo con regularizadores.

Regularizadores en código

Los regularizadores L1 y L2 se encuentran en el módulo regularizers de Keras, no olvides importarlo.

python from tensorflow.keras import regularizers

Definiremos una nueva arquitectura basada en la anterior, para esta ocasión haremos una serie de sutiles cambios que impactarán en el resultado de la red.

En las capas ocultas añadiremos el parámetro kernel regularizer que será un regularizador L2 con valor de 1x10^-5, adicionalmente, después de capa oculta añadiremos el dropout como si fuera otra capa más con un valor de 0.2 refiriéndose a una desactivación del 20% de las neuronas por iteración.

```python model_optimizer = tf.keras.models.Sequential( [tf.keras.layers.Flatten(input_shape = (28, 28, 1)), tf.keras.layers.Dense(256, kernel_regularizer = regularizers.l2(1e-5), activation = "relu"), tf.keras.layers.Dropout(0.2), tf.keras.layers.Dense(128, kernel_regularizer = regularizers.l2(1e-5), activation = "relu"), tf.keras.layers.Dropout(0.2), tf.keras.layers.Dense(len(classes), activation = "softmax")] )

model_optimizer.summary() ```

El resumen del modelo nos mostrará el dropout como si fuera otra capa oculta.

```python Model: "sequential_1"

---

Layer (type) Output Shape Param

flatten_2 (Flatten) (None, 784) 0

dense_4 (Dense) (None, 256) 200960

dropout (Dropout) (None, 256) 0

dense_5 (Dense) (None, 128) 32896

dropout_1 (Dropout) (None, 128) 0

dense_6 (Dense) (None, 24) 3096

================================================================= Total params: 236,952 Trainable params: 236,952 Non-trainable params: 0 ```

Compilaremos y entrenaremos el modelo bajo las mismas directas del modelo pasado para contrastar el rendimiento.

```python model_optimizer.compile(optimizer = "adam", loss = "categorical_crossentropy", metrics = ["accuracy"])

history_optimizer = model_optimizer.fit( train_generator, epochs = 20, validation_data = validation_generator ) ```

Podemos notar en la etapa final que si bien la precisión de entrenamiento bajó un poco, la precisión de validación ha aumentado.

python Epoch 20/20 215/215 [==============================] - 11s 49ms/step - loss: 0.2245 - accuracy: 0.9251 - val_loss: 0.8691 - val_accuracy: 0.7937

Graficaremos los resultados para entender el nuevo desempeño de la red.

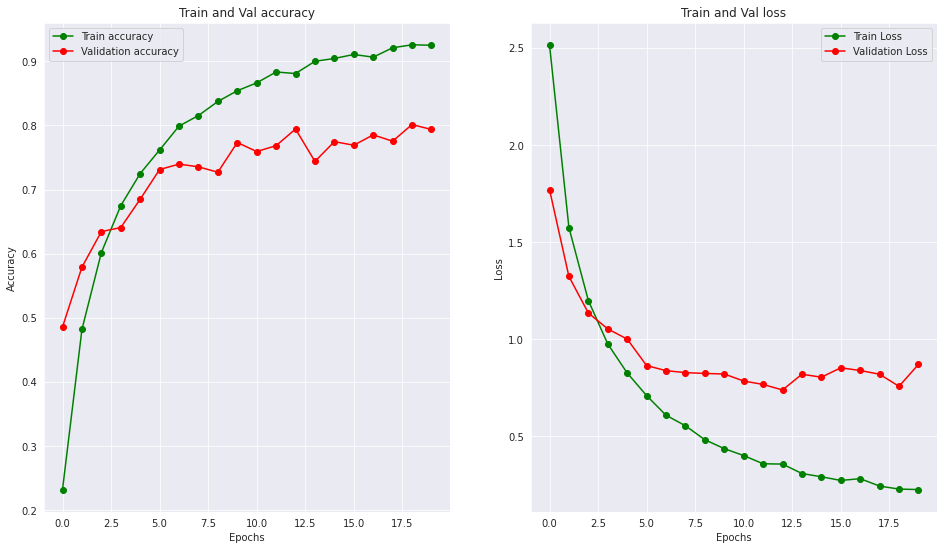
Podemos notar como las gráficas de train y validation ahora tienden a ser más uniformes, esto denota una importante reducción en el overfitting y un incremento en el rendimiento final de la red.

Contribución creada por Sebastián Franco Gómez.