Introducción al lenguaje matemático
¿Por qué importan los símbolos matemáticos?
Lenguaje matemático
Números y variables
Notación científica y prefijos
Quiz: Introducción al lenguaje matemático
Aritmética y geometría
Operadores aritméticos y de agrupación
Operadores de comparación y relación
Símbolos geométricos
Quiz: Aritmética y geometría
Álgebra
Operadores lógicos
Sumatoria y factorial
Conjuntos
Álgebra de conjuntos
Quiz: Álgebra
Cálculo
Notación matemática para cálculo
Notación matemática de la derivada
Quiz: Cálculo
Aplicaciones del lenguaje matemático
Constantes matemáticas
Lectura y escritura de un texto con lenguaje matemático
No tienes acceso a esta clase
¡Continúa aprendiendo! Únete y comienza a potenciar tu carrera
Si ya tienes una cuenta,
Iniciar sesión
Operadores aritméticos y de agrupación
5/15Recursos
Los operadores aritméticos son los símbolos usados para indicar el tipo de operación aritmética que se va a ejecutar.
Tipos de operadores aritméticos
Las diferentes maneras de expresar los operadores aritméticos son los siguientes:
Suma: 3+1
Resta: 4-2
Multiplicación: 3x4, 5*6, (4)(5), 6·7
División: 8÷4, 5:3, 6/3
Jerarquía de los operadores aritméticos
Frecuentemente en una expresión matemática se encuentran varios operadores aritméticos, por ejemplo: 10 - 6 * 9 / 9
Cuando sucede esta situación, los operadores se deben resolver siguiendo este orden:
- Primero la división y multiplicación.
- Luego suma y resta.
Cuando haya dos o más operadores con la misma jerarquía, uno al lado del otro, resolver el que aparezca primero de izquierda a derecha. Por ejemplo:
| Problema | Descripción |
|---|---|
10 - 6 * 9 / 9 |
se resuelve la multiplicación |
10 - 54 / 9 |
se resuelve la división |
10 - 6 |
se resuelve la resta |
4 |
Operadores de agrupación
La primera vez que se utilizó un signo de agrupación fue en 1399, en este caso el punto ., pero fue hasta 1470 que se usó por primera vez el paréntesis para agrupar elementos. Hubo otros intentos, como Giuseppe Peano y el uso de los puntos “. … …” o John Wallis y su “vinculum”. Actualmente, se usan los paréntesis, corchetes y llaves.
Jerarquía de los operadores
Además de los operadores aritméticos, también nos encontramos con otros operadores como la raíz y la potencia. Cuando una expresión matemática contenga varios operadores, se resuelven en el siguiente orden:
- Paréntesis
- Corchetes
- Llaves
- Potencia y raíz
- División y multiplicación
- Suma y resta
Ejemplo:
| Problema | Descripción |
|---|---|
{2·(4-3)}/5 |
se resuelve la resta |
{2·1}/5 |
se resuelve la multiplicación |
2/5 |
se resuelve la división |
En teoría se tendría que escribir en la parte más interna los paréntesis, después los corchetes y por último las llaves; pero, no todos siguen esta convención, así que lo más recomendado es que primero se realice lo que esté más en el centro de la operación hasta llegar a los extremos.
Símbolos combinados o alterados
Estos son útiles para la precisión de aproximaciones en cálculo (aproximación por la izquierda o la derecha), tolerancias mecánicas, o para mostrar dos ecuaciones en una, por ejemplo:
- ±
- ∓
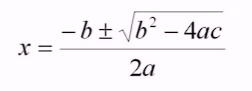
Contribución creada por: Néstor Arellano y Avilio Muñoz Vilchez.
Aportes 27
Preguntas 1
Ordenar por:
Para la precisión de aproximaciones, ¿a qué se refiere Marisol si te acercas por la derecha o la izquierda? Ejemplo:
Aquí existe un límite donde se parten las líneas, es el punto a, ese LÍMITE ES IGUAL AL PUNTO a QUE SE PINTA EN X, mientras que las otras líneas solamente están demasiado cerca, por lo que si te aproximas desde la derecha o la izquierda te da diferentes valores en Y, por eso saber desde donde te aproximas es importante.
El acrónimo PEMDAS es una ayuda muy útil para recordar el orden las operaciones
Comparto mis resultado del reto 😃
Reto completado, siempre es bueno repasar estos conceptos 😄.
-
a) 5
-
b) 23
-
c) 12
-
d) 57
-
e) 7
Lo bueno, es que este tema en específico, desde chica se me ha facilitado y me gusta mucho realizar ejercicios así 😄
reto terminado 5 de 5 ヾ(≧▽≦*)o al fin
“La entonación le daba significado a las palabras”, cosa que no se ha sistemátizado en las aplicaciones que leen por ejemplo PDF. que todavía suenan muy por debajo de la calidadd requerida. Y hay aplicaciones de audiolibros que tienen que ser grabados por personas todavía.
Reto 😃
a) 4 + 8 ÷ 2 − 3=5
b) 19 + (22 − 8 × 2) − 2=23
c) 5 − 4 + 2(2 − 1) + 9=12
d) 2 + 6(2 × 5) − 10 ÷ 2=57
e) {20 + [5 − 60 ÷ 3 + 2(4 − 3)]}=7
Los operadores aritméticos se utilizan para realizar operaciones matemáticas básicas en programación, como la suma (+), la resta (-), la multiplicación (*), la división (/) y el módulo (%).
Los operadores de agrupación, como los paréntesis (), se utilizan para agrupar expresiones y establecer el orden de evaluación en las operaciones aritméticas. Las expresiones dentro de los paréntesis se evalúan primero, seguidas de las multiplicaciones y divisiones, y finalmente las sumas y restas.
Muy bueno recordar la jerarquía de operaciónes.
También los símbolos combinados pueden servir para hacer acotaciones
Todo un repaso. Gracias Marisol.
Resultados:
a) 4 + 8 ÷ 2 − 3 = 4 + 4 - 3 = 5
b) 19 + (22 − 8 × 2) − 2 = 19 + (22 - 16) - 2 = 19 + 6 - 2 = 23
c) {5 − 4 + 2(2 − 1) + 9} = {5 - 4 + 2(1) + 9} = 1 + 2 + 9 = 12
d) {2 + 6(2 × 5) − 10 ÷ 2)} = {2 + 6(10) - 5} = 2 + 60 - 5 = 57
e) {20 + [5 − 60 ÷ 3 + 2(4 − 3)]} = {20 + [5 - 20 + 2(1)]} = 20 - 13 = 7
e)
{20 + [5 − 60 ÷ 3 + 2(4 − 3)]}
20 + [ 5 - 20 + 2(1)
20 + (-15) + 2
5+2
7
Respuestas del reto propuesto:
a) 5
b) 23
c) 12
d) 57
e) 7
a) 4 + 8 ÷ 2 − 3 = 5
b) 19 + (22 − 8 × 2) − 2 = 23
c) {5 − 4 + 2(2 − 1) + 9 = 12
d) {2 + 6(2 × 5) − 10 ÷ 2) = 57
e) {20 + [5 − 60 ÷ 3 + 2(4 − 3)]} = 7
5 de 5 en reto , pero es muy gracioso ver en que hay calculadoras que no respetan estas reglas y dan resultados muy diferentes
3 de 5 en el reto.
Me confundí un poco con el cuarto ejercicio.
Pero ahora lo tengo todo claro.
Que bueno repasar!
Me encanta el aporte histórico de estas clases.
En este reto obtuve 4 respuestas de 5, pero al fin entendí las jerarquías y como resolver ejercicios cuando tenga dos operaciones con la misma jerarquía, y así no morir en el intento. Ok, no.
En el reto 3 el inciso c) y d) les faltó la llave de cierre. otro error de dedo.
¿Quieres ver más aportes, preguntas y respuestas de la comunidad?
o inicia sesión.