RMSE y R cuadrado para evaluar modelos de regresión
Clase 17 de 20 • Curso de Fundamentos de AI para Manejo de Datos
Contenido del curso
Modelo Predictivo
Tipos de Aprendizaje
- 6

Aprendizaje supervisado: regresión y clasificación en machine learning
05:20 min - 7
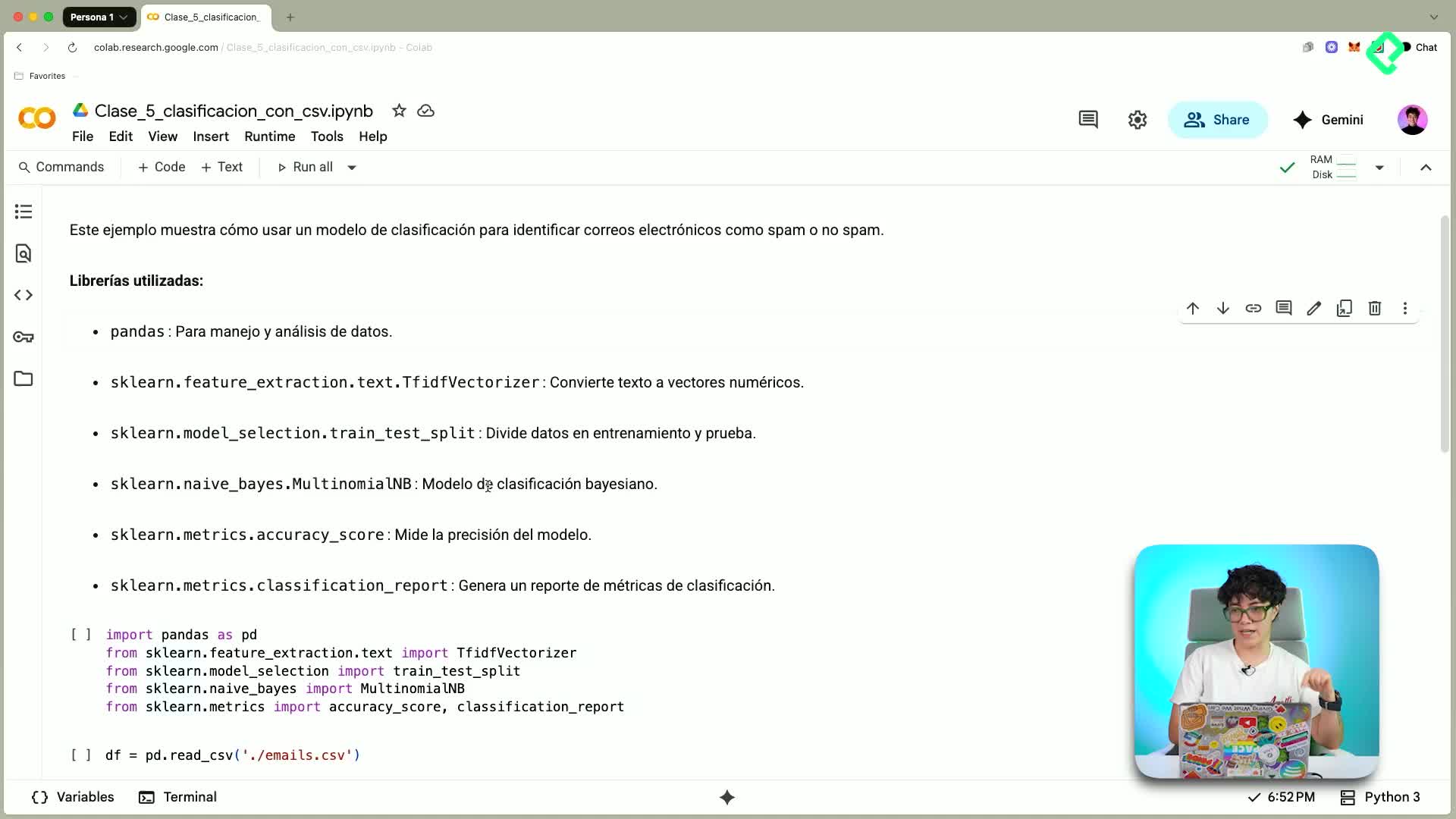
Detección de spam con Python y Google Colab
10:12 min - 8

Clustering y normalización de datos con K-means
08:42 min - 9

Reducción de dimensionalidad con PCA para análisis de datos
06:50 min - 10

Aprendizaje por refuerzo con Q-learning y OpenAI Gym
11:24 min
Herramientas para IA
Ciclo de Vida ML
Ética en IA
Resumen
Objetivo del profesor
El objetivo de esta clase era que los estudiantes comprendieran dos métricas fundamentales para evaluar modelos de regresión: RMSE (Root Mean Square Error) y R² (coeficiente de determinación), incluyendo cómo calcularlas, interpretarlas y utilizarlas de manera complementaria para evaluar el rendimiento de modelos de machine learning.
Habilidades desarrolladas
- Evaluación de modelos: Capacidad para medir y comparar el rendimiento de diferentes modelos de regresión
- Interpretación de métricas: Habilidad para entender qué significan los valores de RMSE y R² en contextos específicos
- Programación en Python: Implementación práctica de cálculos de métricas usando librerías como scikit-learn
- Análisis comparativo: Capacidad para evaluar múltiples modelos y determinar cuál es más adecuado
- Pensamiento crítico: Comprensión de que ninguna métrica cuenta toda la historia por sí sola
Conceptos clave
- RMSE (Root Mean Square Error): [00:08] Raíz del error cuadrático medio que mide el tamaño promedio de los errores en las mismas unidades que la variable objetivo
- R² (R cuadrado): [00:12] Coeficiente de determinación que mide qué proporción de la variabilidad de los datos puede explicar el modelo
- MSE (Mean Square Error): [01:18] Error cuadrático medio, paso intermedio para calcular RMSE
- Elevación al cuadrado: [01:04] Técnica para eliminar signos positivos y negativos de los errores
- Variabilidad: [02:01] Dispersión de los datos que el modelo intenta explicar
- Relación lineal fuerte vs débil: [04:02] Diferentes grados de correlación entre variables
- Análisis de residuos: [08:06] Método complementario para evaluar modelos
Palabras clave importantes
- Métricas de evaluación
- Error cuadrático medio
- Coeficiente de determinación
- Predicciones vs valores reales
- Sobreajuste (overfitting)
- Validación cruzada
- Regresión lineal
- Variables objetivo
- Residuos
Hechos importantes
- [01:26] La elevación al cuadrado evita que errores positivos y negativos se cancelen
- [01:39] Un RMSE de 20,000 en predicción de precios de casas puede ser bueno o malo dependiendo del contexto (bueno para casas de 3 millones, malo para casas de 50,000)
- [02:08] Un R² cercano a 1 significa que el modelo explica casi toda la variabilidad
- [02:13] Un R² cercano a 0 significa que el modelo explica muy poco, casi como adivinar al azar
- [02:17] Un R² alto no garantiza que el modelo sea útil si no se cumplen los supuestos de regresión
- [08:02] Ninguna métrica cuenta toda la historia por sí sola; se necesita análisis conjunto
Datos principales del experimento
- [03:13] Semilla aleatoria: 42
- [03:18] Número de observaciones: 200
- [05:25] Modelo lineal fuerte: MSE = 0.934, RMSE = 0.96, R² = 0.97
- [07:07] Modelo lineal débil: MSE = 16.1, RMSE = 4.03, R² ≈ 0 (cercano a cero)
- [07:34] Modelo no lineal: MSE y RMSE más altos, pero R² con mayor capacidad explicativa que el modelo débil