P vs NP: el problema más difícil explicado con viajes en el tiempo

A principios de este siglo el Instituto Clay de Matemáticas enunció siete problemas. Los problemas del milenio.Uno de ellos se llama P vs NP. El único problema relacionado con la computación que se encuentra en esta lista.

En este artículo te explico el problema más complejo de las Ciencias de la Computación. Y no necesitas programar para comprenderlo. Entenderás las bases de este impresionante problema, usaremos los viajes en el tiempo como ejemplo, te contaré de su relevancia en el futuro cercano como, ¿qué sucede si se resuelve? y un curso de Platzi al terminar.
Empecemos.

La máquina del tiempo y cómo entender el problema de P vs NP

Supongamos que construí una máquina del tiempo que anuncia que para 2030 la humanidad habrá llegado a Marte.

Te cuento que viajar en el tiempo como problema es difícil de resolver. Me tomó mucho tiempo estudiando temas de Computación, Física y Matemáticas. Fue muy difícil…

Sin embargo, tú dudas que esto sea cierto, y, por lo tanto, te haces la pregunta: ¿cómo puedo comprobar que esta máquina del tiempo funciona? Si acabo de contarte que en 2030 sucede algo importante, podrías esperar hasta que estemos en el año 2030 y comprobarlo. Si digo “en 2025, el evento X sucede”, entonces puedes esperar hasta el 2025 y verificar si ese evento realmente pasa.

Y podemos repetir la misma lógica, si se trata de un evento del siguiente mes, la siguiente semana, o mañana mismo.Por lo tanto, parece sencillo verificar si una máquina del tiempo funciona.

Otra pregunta más. Si es fácil comprobar que mi máquina del tiempo funciona, ¿también sería fácil construir una máquina del tiempo?
Entonces, comparemos estos dos problemas:

“Construir una máquina del tiempo”
“Verificar que una máquina del tiempo funcione”

Es casi un hecho que “verificar que una máquina del tiempo funcione” es un problema más sencillo. Pero (y no hay respuesta correcta), ¿significa que “verificar que funcione” es también tan fácil cómo “construir y que funcione”?
En mi opinión personal no. Pero, ¿tú qué crees?

Ahora llevemos a esto a un plano más realista.
—
Podemos pensar en los inicios de la computación como en el desarrollo de una calculadora. Hoy es imperceptible por la rapidez con la que funcionan, pero incluso cuando sumas 2 más 3 hay un tiempo entre que ejecutas tu operación y obtienes la respuesta.

Un tiempo muy pequeño. Quizás sean microsegundos. Pero si en lugar de 2 y 3, fuesen números con centenas de dígitos tomaría segundos, y con miles de dígitos tomaría minutos, y con millones de dígitos tomaría hasta horas.

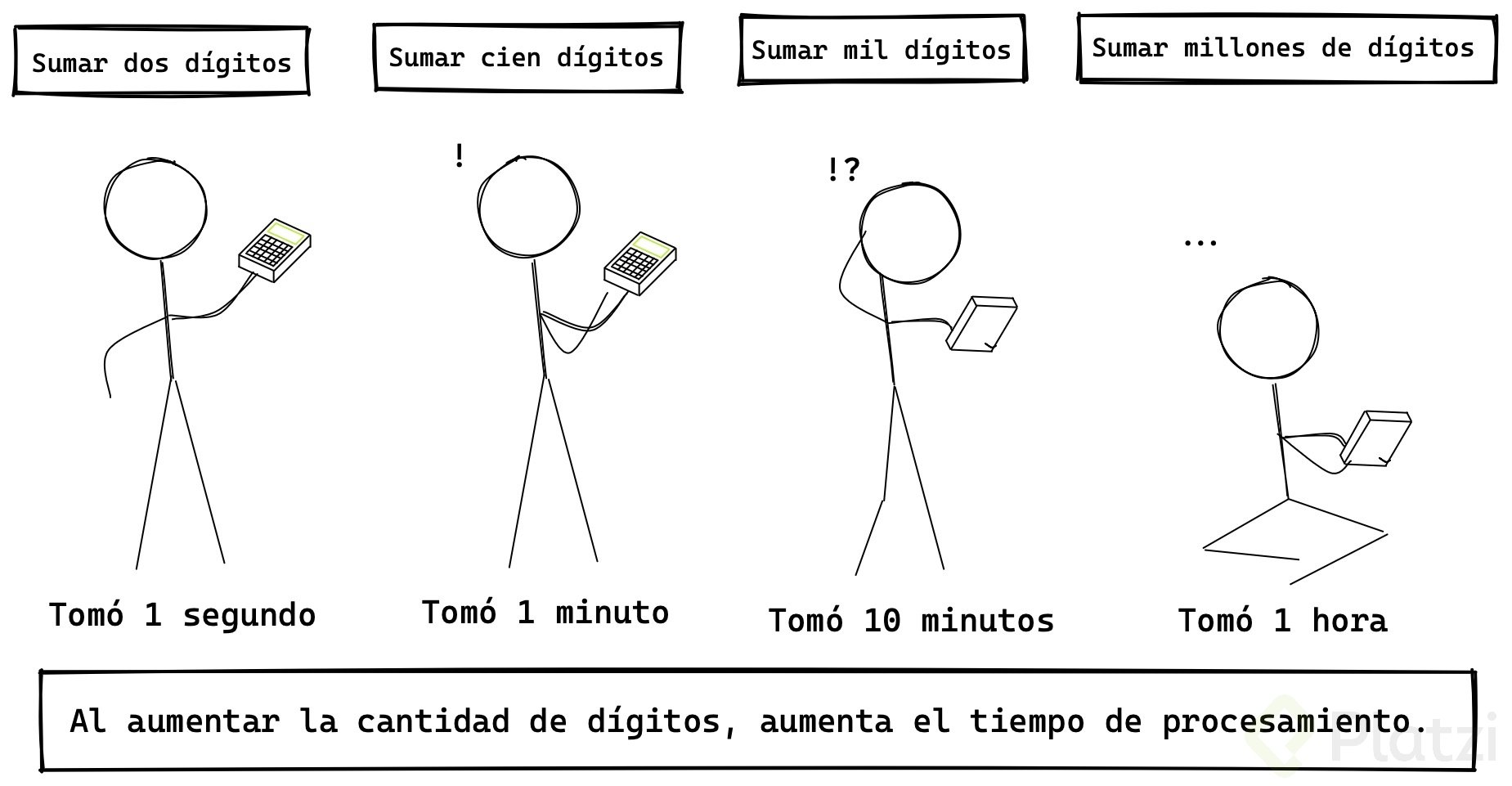
¿Ves el patrón? Mientras más grande es nuestra operación matemática, el tiempo para realizar una operación aumenta. Hay una correlación directa:

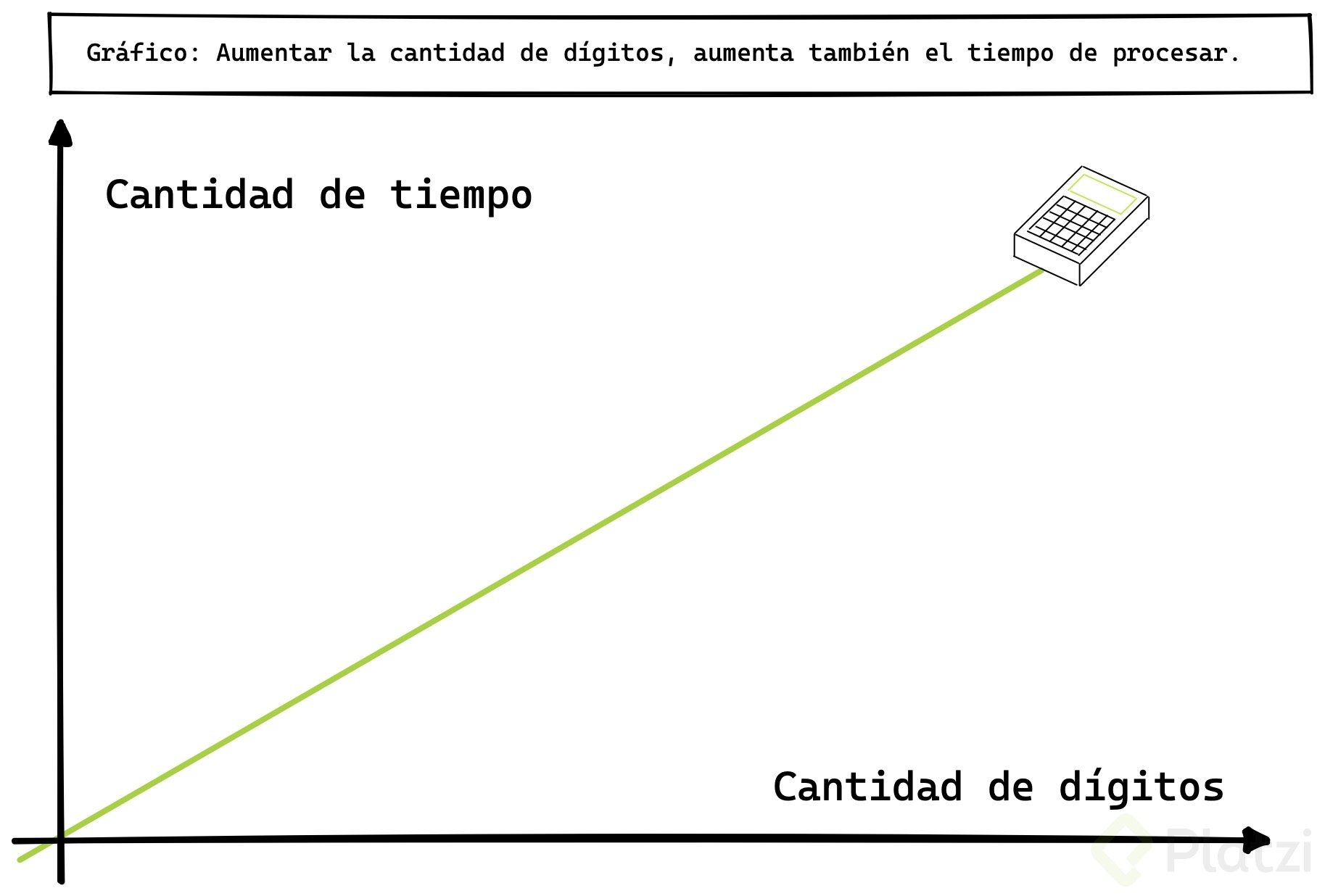
Y podemos plantearnos un cálculo mucho más difícil, es decir, un cálculo que le tome mucho más tiempo a la calculadora para resolverlo.
Por ejemplo: una operación de sumar no dos números, sino una cantidad de números que se incremente de forma exponencial (es decir: 1, 2, 4, 8, 16), llegará a un punto donde operar y generar un resultado puede verse así:

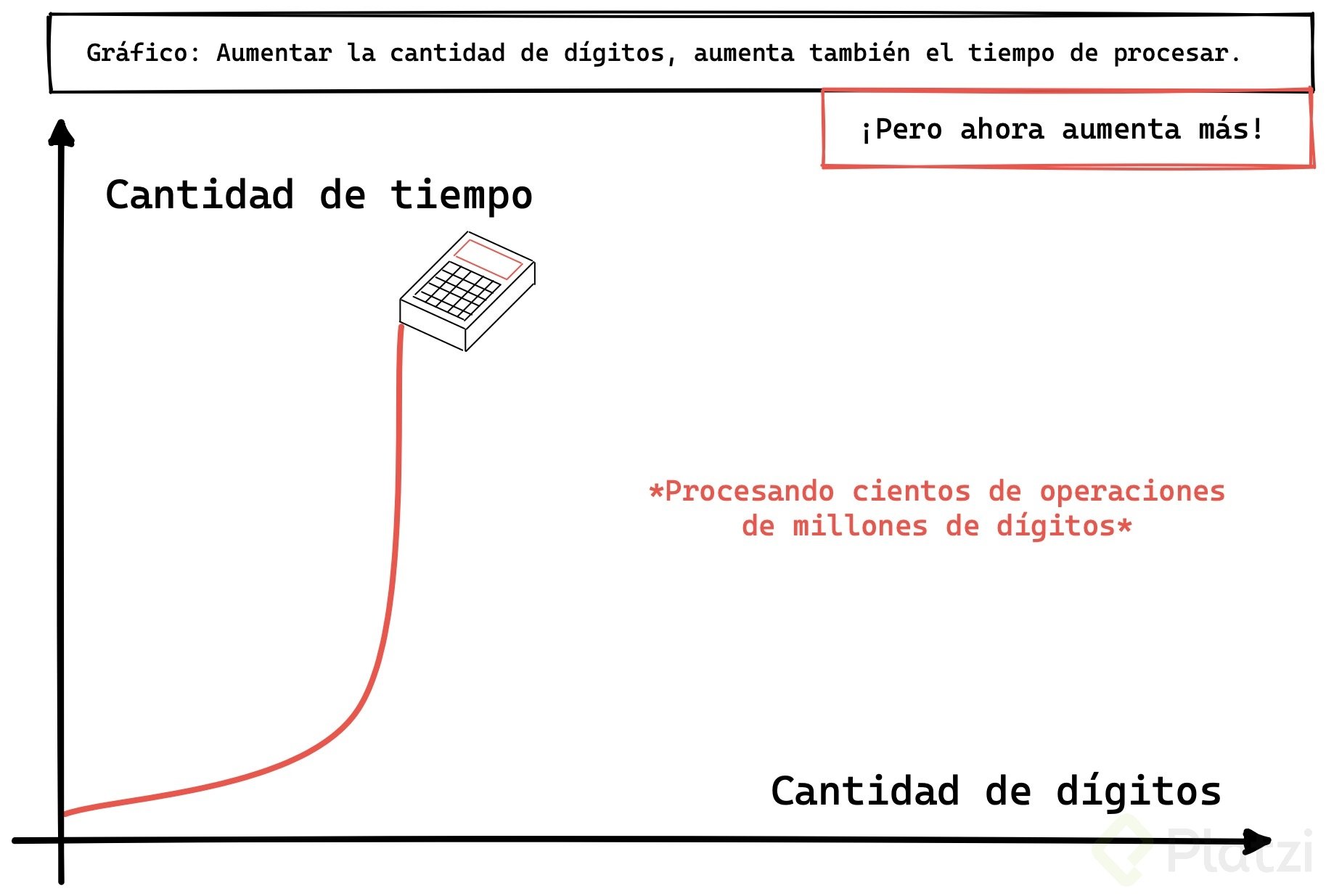
Esto último no es un problema imposible de ejecutar, pero sí muy difícil si el resultado lo queremos durante nuestro tiempo de vida, donde una calculadora (o una computadora) podría tardar años en dar una respuesta.

Mientras tanto, ejecutar 2 más 3, ni es imposible ni es difícil.

Ya tendremos más tiempo en un curso para ahondar en lo que significaron los dos gráficos anteriores.
Hay una forma más simple de verlo. En este contexto, podemos dividir problemas: unos cuya solución es posible, y otros cuya solución es posible y además es fácil.

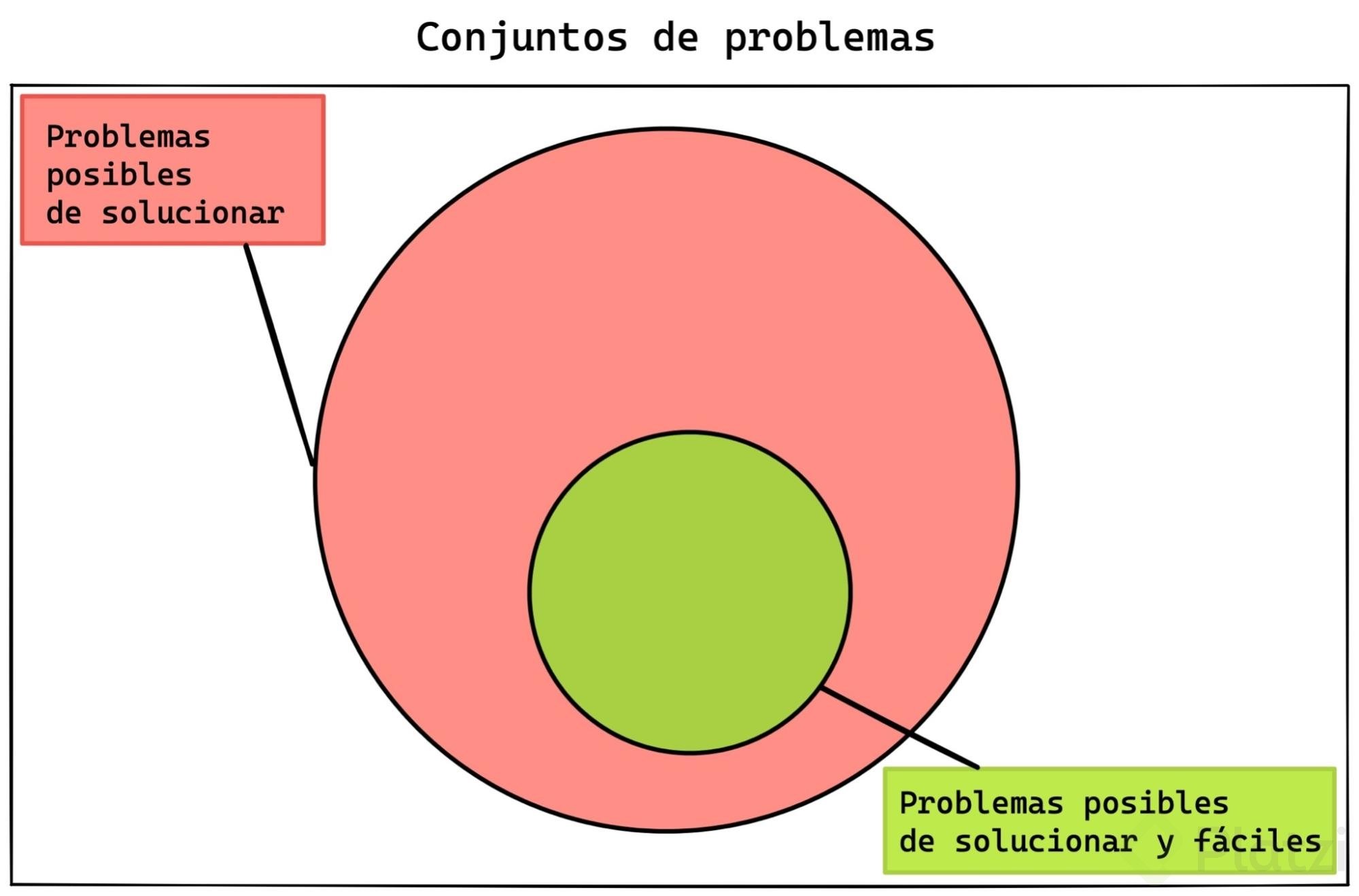
A los problemas posibles de solucionar y fáciles de solucionar los llamaremos P. Y a todo el conjunto NP.

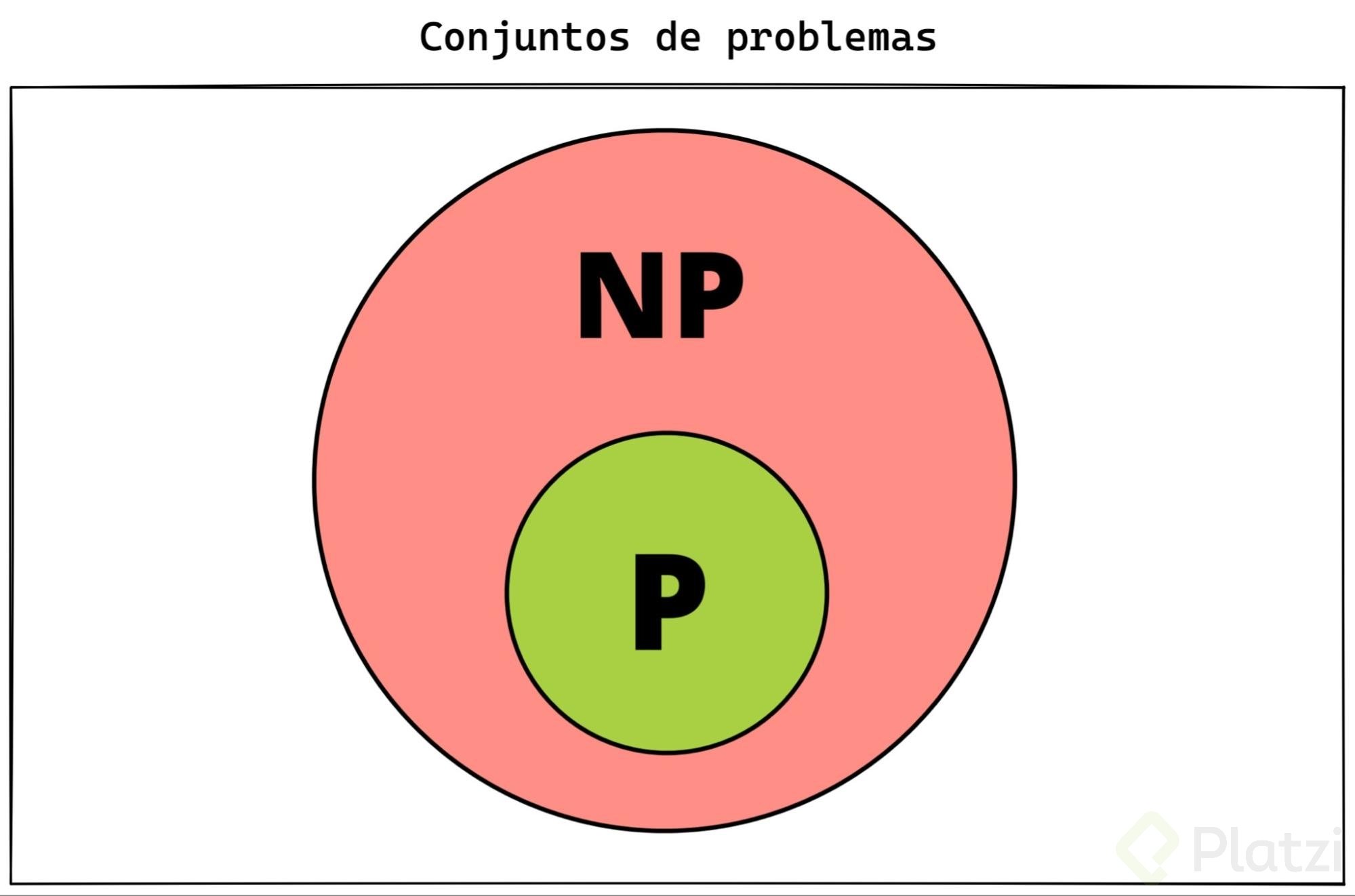
¿Por qué se usa P y NP?

P es por Polinomial y NP por No-Determinista Polinomial.

Cuando medimos la dificultad en hallar la solución a un problema, o incluso cuando medimos qué tan eficiente es una solución a un problema, vamos a ver una palabra: Polinomial. Es uno de los muchos resultados que podemos obtener, y qué nos cuentan “¿qué tan difícil es realizar una determinada acción en computación?”.

P contiene problemas cuya solución es fácil.
NP contiene problemas difíciles, pero donde verificar soluciones es fácil.
No-Determinista significa que a veces tenemos que probar muchas posibles soluciones antes de encontrar la correcta.

Esto puede empujarnos a usar estrategias diferentes, incluso el azar. Es como armar un rompecabezas gigante, y probar unir diferentes piezas hasta que encajen, sin un orden, simplemente al azar.

Solamente imagina que existe una gran cinta métrica que nos cuenta esa dificultad. Piensa en un problema que escapa de P como un nivel de dificultad muy alto. Como esto:

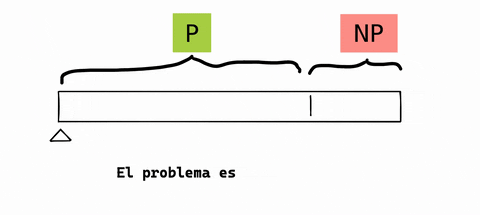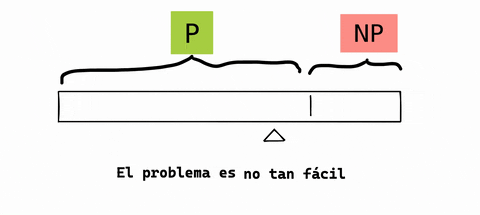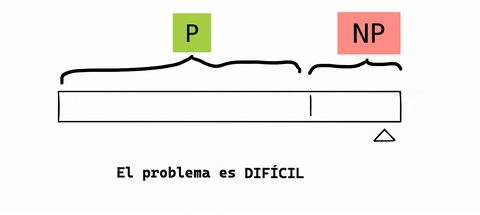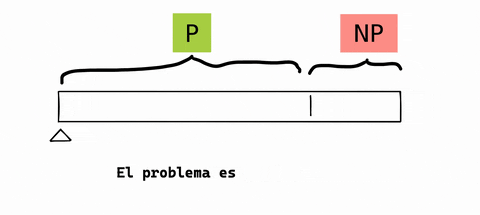
Explicación del problema P vs NP

Volvamos a la pregunta del principio: verificar que una máquina del tiempo funcione o construir una máquina del tiempo. ¿Son problemas igual de sencillos?
Supongamos que no lo son. En nuestro mundo semi-real podríamos encajar estos dos problemas así: NP contendría “verificar la máquina del tiempo” y P “construir la máquina del tiempo”:

Pero, ¿y si verificar problemas SÍ resulta ser tan fácil como solucionarlos? En ese caso, el anterior gráfico no sería correcto. Por lo tanto, P y NP serían un solo conjunto y debería verse así:

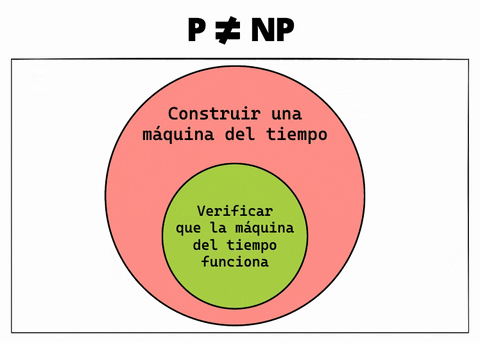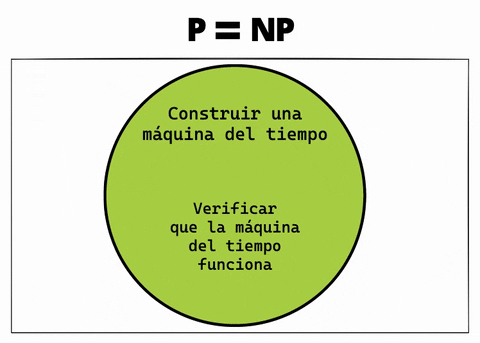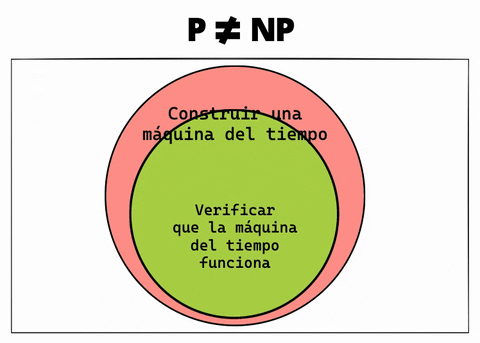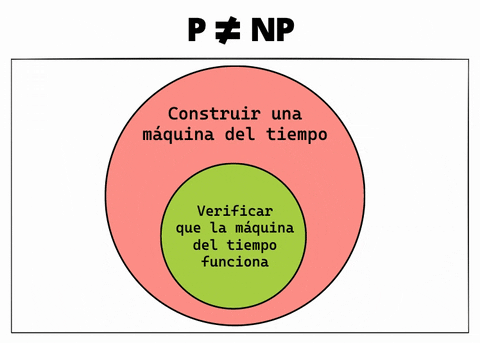
Y así es como construir una máquina del tiempo se convierte en algo fácil.
El problema del milenio pregunta esto: ¿es P es igual a NP?

Una gran parte de la comunidad científica responde que no son el mismo conjunto de problemas (P ≠ NP). Pero hasta ahora no existe una forma de probar esto.

Relevancia del problema P vs NP

Resolver esta pregunta sería un gran avance en las ciencias de la computación y el impacto variaría dependiendo de la respuesta. Un futuro donde P ≠ NP, es muy parecido al que vivimos hoy en día (es la teoría más aceptada). Pero un futuro donde P = NP abriría la puerta al desarrollo de algoritmos más eficientes en problemas que hoy en día son difíciles de resolver.

Incluso, podría significar que la criptografía actual no sería segura. El algoritmo RSA, que es el más usado en la actualidad para cifrar información, es un algoritmo que basa esa seguridad en la dificultad de resolver una operación matemática, y lo fácil que es verificar esa operación. Pero si de pronto P = NP, entonces RSA no sería seguro, y habría que migrar a una nueva forma de cifrar información.

De pronto y el único límite de la computación sería la potencia de una máquina, y poco más. O quizás, existen problemas que siempre serán difíciles de resolver. Pero, ¿cómo saberlo?
¿Qué sucede con los viajes en el tiempo? Realmente no influyen aquí. — P vs NP se enfoca únicamente en problemas de decisión. Es decir, problemas cuya respuesta es “Sí” o “No”. Quizás podríamos formularlo como “¿es posible viajar en el tiempo?”. Pero es un escenario ficticio.

En la vida real, conocer la mejor solución, es decir, el mejor algoritmo para resolver un problema, es muy importante. Sobre todo si estudias ingeniería de software. En este artículo te introduje un tema muy interesante: complejidad algorítmica, pero queda mucho más por profundizar.

En el curso de Complejidad Algorítmica con JavaScript, no instalarás ninguna librería o framework, trabajaremos en las bases teóricas en torno a la pregunta ¿qué solución es mejor para abordar un problema?, te contaré sobre los recursos estudiados en la evaluación de algoritmos, aprenderás notación Big-O y a comparar algoritmos en código.