Polinomios
Un polinomio es una expresión matemática con términos algebraicos. Un término algebraico está conformado por un coeficiente y una variable:
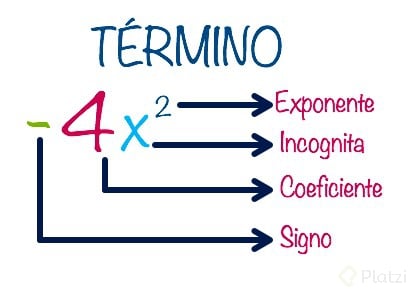
NOTA: Cuando tenemos un monomio como x2, seguimos teniendo un coeficiente, el cuál es 1, pero al ser una unidad no se escribe. Lo mismo ocurre con la variable x, cuándo la encontramos así significa que su exponente es 1, pero como nuevamente estamos hablando de una unidad no hace falta indicarlo.
Tipos de polinomios:
- Polinomio de un término: monomio, por ejemplo, 8xy.
- Polinomio de dos términos: binomio, por ejemplo, 8xy - 2y.
- Polinomio de tres términos: trinomio, por ejemplo, 8xy - 2y + 4.
- Cuando tenemos más de 3 términos lo llamamos polinomio directamente.
¿Qué es el grado de un polinomio?
El grado de un polinomio de una sola variable es el exponente más grande. El grado de un polinomio con más de una variable es determinado por el término con el exponente más grande (también se conoce como exponente mayor). La complejidad de un polinomio está indicada por su grado. Miremos algunos ejemplos:
-
3x: grado 1
-
8xy: grado 2 (x:1 + y:1= 2)
Apuntes extra:
- Los polinomios deben estar ordenados. Por ejemplo, si tenemos el polinomio 3x3 + 5x4, debemos ordenarlo por el valor de su exponente: 5x4 + 3x3. Además, debemos agregar los demás términos ordenándolos por el valor de su exponente, por lo que quedaría: 5x4 + 3x3 + 0x2 + 0x + 0.
Simplicar polinomios y términos semejantes
Los polinomios se pueden volver muy extensos y simplificarlos es una excelente manera de hacerlos más legibles, y se simplifican a través de los términos semejantes. Los términos semejantes son términos que comparten la parte literal, que está conformada por la **variable **y su exponente.
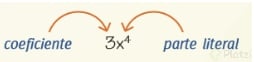
Operaciones con términos semejantes:
Ya sabemos qué son los términso semejantes, pero todavía no sabemos simplificar. A continuación las operaciones para hacerlo:
- En la multiplicación y división solo importa que los términos compartan la variable, no el exponente.
- En la suma y resta SÍ o SÍ deben compartir la parte literal (variable y exponente) los términos para realizar la operación.
Propiedad distributiva:
Se trata de una de las propiedades de la multiplicación que se aplica respecto a una suma o a una resta. Dicha propiedad indica que dos o más términos presentes en una suma o en un resta multiplicada por otra cantidad, resulta igual a la suma o la resta de la multiplicación de cada uno de los términos de la suma o la resta por el número.
Factor común:
El factor común es un de los métodos de factorización más utilizados y está basado en la propiedad distributiva de los números reales; pero de forma contraria.
En la imagen, como la factorización ha sido expresado como el factor común: «a» multiplicado por otro factor: «(b+c)». Vemos que «a» es esa variable que está presente en cada término, y eso es a lo que nos referimos con factor común.
NOTA: El factor común aplica para todas las expresiones, a los números, las letras, todo.
Después de conocer la definición y la figura que se muestra, podemos decir que no será muy complicado reconocer el Factor Común en un Polinomio. Por último, un ejemplo:
Ejemplo:
- Polinomio: 5ab + 7a
- Polinomio luego de la Factorización: a(5b + 7)
