Leyes de Exponentes: Potencia de Potencia y Radicación

La potencia y la radicación son operaciones matemáticas fundamentales que nos permiten realizar cálculos, simplificar expresiones y modelar fenómenos en diversas disciplinas.

¿Qué es la potencia de una potencia?

La potencia de una potencia se refiere a elevar una base a un exponente, y luego elevar ese resultado a otro exponente. Esencialmente, estamos multiplicando exponentes y simplificando las expresiones resultantes.

Ejemplo de potencia de una potencia: (x^2)^3 = x^6

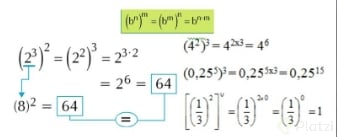
Reglas de potencia de una potencia

Tendremos una base elevada a una potencia y al mismo tiempo todo esto estará encerrado en un paréntesis y elevado a otra potencia. La regla consiste en multiplicar ambos exponentes.

La ley de potencia de una potencia establece que, al elevar una potencia a otra potencia, se multiplica los exponentes. La expresión general de esta ley es la siguiente:

(a^m)^n = a^(m*n)

¿Qué son las leyes de los exponentes?

Ejemplos de potencia de una potencia

Para comprender mejor la potencia de una potencia, veamos algunos ejemplos prácticos que ilustran cómo aplicar estas propiedades en diferentes situaciones. En cada ejemplo, calcularemos el resultado de la expresión dada y explicaremos los pasos involucrados.

Ejemplo 1: (2^3)^4(2^3)^4

Comencemos con un ejemplo simple. Tenemos la expresión (2^3)^4(2^3)^4, lo que significa que debemos elevar 2 al cubo y luego elevar ese resultado a la cuarta potencia. Veamos cómo resolverlo:

(2^3)^4=2^3⋅4=2^12

Aquí, aplicamos la propiedad de potencia de una potencia de la misma base y multiplicamos los exponentes para obtener 12. Por lo tanto, el resultado final es 2^12.

Ejemplo 2: (5^2)^3

En este ejemplo, tenemos la expresión (5^2)^3. Siguiendo los pasos adecuados, evaluemos esta expresión:

(5^2)^3=5^2⋅3=5^6

Nuevamente, utilizamos la propiedad de potencia de una potencia de la misma base para multiplicar los exponentes y obtener 6. Por lo tanto, el resultado final es 5^6.

Ejemplo 3: (3^4)^2

Continuemos con otro ejemplo interesante. Aquí, la expresión dada es (3^4)^2. Veamos cómo simplificarlo:

(3^4)^2=3^4⋅2=3^8

Una vez más, aplicamos la propiedad de potencia de una potencia de la misma base y multiplicamos los exponentes para obtener 8. Por lo tanto, el resultado final es 3^8.

¿Cómo simplificar una expresión de potencia de una potencia?

Para simplificar una expresión de potencia de una potencia, debemos aplicar las propiedades adecuadas. Si las bases son iguales, podemos multiplicar los exponentes juntos. Si las bases son diferentes, debemos tratar cada base por separado y aplicar las reglas correspondientes.

¿Qué es la radicación?

La radicación es la operación inversa a la potencia. Nos permite encontrar el número que, elevado a un exponente determinado, produce un resultado específico. En la expresión √25, el símbolo de raíz cuadrada (√) nos indica que debemos encontrar el número que, elevado al cuadrado, sea igual a 25. En este caso, el resultado es 5, ya que 5^2 = 25.

Reglas de radicación

Cambiamos de una raíz a una fracción y viceversa. Es importante saber que siempre que encontremos una expresión en forma de raíz es mejor pasarla a fracción para que se nos haga más fácil operarla. La regla consiste en que en exponente de la base va a ser nuestro numerador y el radical de nuestra raíz será el denominador.

¿Cuál es la diferencia entre la potencia y la radicación?

La potencia es una operación que implica multiplicar un número por sí mismo un cierto número de veces, mientras que la radicación es la operación inversa, en la cual encontramos el número que, elevado a una potencia específica, produce un resultado dado.

Contribución creada con los aportes de: Mayra López y Héctor Gerardo García Escobar.

Repasa: qué es el lenguaje algebraico