Los problemas de optimización surgen en casi toda actividad humana, y es que siempre queremos encontrar la mejor manera de hacer las cosas. Por ejemplo, cuando practicamos algún deporte como fútbol ⚽️ nos gustaría maximizar nuestro número de goles, así como minimizar el número de faltas que cometemos. O bien, si somos dueños de una empresa siempre estaremos interesados en obtener la mayor ganancia. A veces es posible formular situaciones a optimizar de modo que implique maximizar o minimizar una función.
Si estás leyendo estas líneas es porque ya tuviste un primer acercamiento a este tema con el Curso de Cálculo para Análisis de Datos. Aprovecharemos este post para profundizar en el mundo de la optimización.
Para comenzar, debemos establecer que maximizar (o minimizar) una función significa encontrar valores en el dominio de la función en los cuales ésta alcance su valor máximo (o mínimo). Así que, empecemos definiendo cómo entendemos estas palabras en matemáticas.

Ya han empezado a salir algunas definiciones matemáticas, pero no hay que alarmarnos, las definiciones anteriores pueden quedar mejor expresadas con las siguientes imágenes: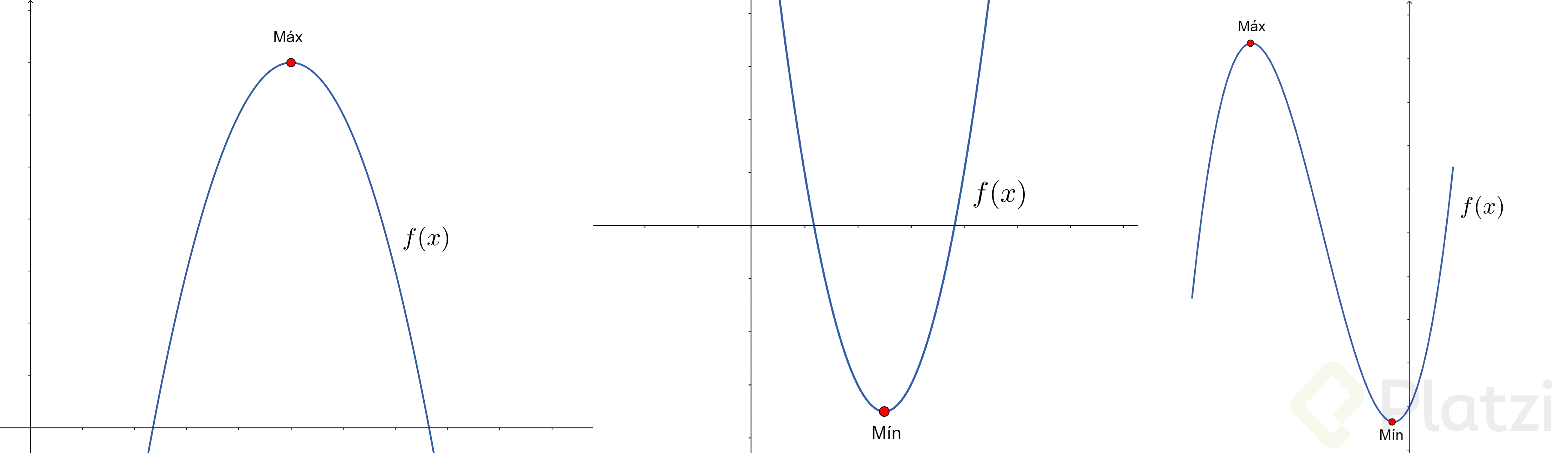
A partir de aquí es posible que surja la pregunta: ¿Las funciones siempre tienen un valor máximo (o mínimo)? La respuesta es que si la función que estudiamos es continua (aquella de la que podemos representar su gráfica de un solo trazo) en un intervalo de números [a, b], entonces ésta siempre alcanza un valor máximo y uno mínimo en dicho intervalo. Para saber cómo encontrar dichos valores debemos poner atención en los puntos críticos.

Ahora que ya sabemos dónde buscar, podemos dar una serie de pasos a seguir para encontrar los valores extremos:
Determinamos todos los puntos críticos de la función en el intervalo.
Evaluamos en la función todos los puntos críticos.
El más grande y el más pequeño de los valores evaluados serán el valor máximo y el valor mínimo absoluto de la función en ese intervalo.
Con las definiciones y pasos anteriores ya estamos listos para optimizar una función. Pongamos lo aprendido en práctica mediante un ejemplo:
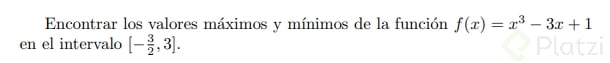
De acuerdo a los pasos que debemos seguir, primero determinaremos todos los puntos críticos en el intervalo. La derivada de la función es:
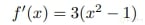
Desempolvando un poco nuestros conocimientos de álgebra podemos concluir que los puntos estacionarios son x=1 y x=-1; para esta función podemos decir que no existen puntos singulares. Así, el conjunto de puntos críticos es {-3/2, -1, 1, 3}. Seguimos con nuestros pasos, ahora evaluando todos los puntos críticos en nuestra función:
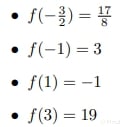
Así el valor mínimo es -1, el cual se alcanza en x=1 y el valor máximo es 19 que se alcanza en x=3.
Ya sabemos resolver una clase, aunque reducida, de problemas de optimización. Sin embargo, debemos tener en cuenta que no siempre vamos a querer optimizar sobre un intervalo cerrado, cuando esto suceda tendremos que ir en la búsqueda de valores máximos y mínimos locales con ayuda de los criterios de la primera y la segunda derivada.
Hasta aquí ha llegado este tutorial y antes de despedirnos me gustaría comentarte que el cálculo es sólo una de la gran cantidad de herramientas de las que hace uso la optimización, así que si quieres profundizar en otras técnicas o en los criterios mencionados déjamelo saber en los comentarios para que platiquemos sobre estos temas, y ya sabes ¡nunca pares de aprender matemáticas!💚💚💚
📕 📚 Bibliografía
Louis Leithold. (2009). EL CÁLCULO. México: Oxford University Press.
James Stewart. (2008). Cálculo diferencial e integral. México: CENGAGE Learning.
