La hipotesis de Riemann es uno de los problemas matematicos aun sin resolver mas interesantes. Ha cautivado la imaginación de muchas personas en el mundo por su ubiquidad, practicamente aparece en situaciones inesperadas y al momento de encontrarse su solución, una miriada de otras cuestiones seran tambien resueltas.
La motivación. He realizado esta traducción con el objetivo de ayudarme a mí mismo a entender el planteamiento de la hipótesis y así tratar de extraer la belleza detrás del misterio, que aun hoy en día, después de varias generaciones sigue sin resolver (161 años). Lo hago aquí por si acaso a alguien más le interesa el tema y le resulta útil leer esto en español. Las ecuaciones han sido escritas en laTex y convertidas en archivos de imagen gracias a Codecogs. La traducción ha sido realizada usando google traductor y revisada manualmente para ajustar algunos términos que suelen confundir al traductor automático. — Luisca.
Creo que puedo expresar mi agradecimiento por el honor que la Academia me ha otorgado hasta cierto punto, a través de mi admisión como uno de sus corresponsales, si uso rápidamente el permiso recibido para comunicar una investigación sobre la acumulación de números primos; un tema que tal vez no parece ser totalmente indigno de dicha comunicación, dado el interés que Gauss y Dirichlet han mostrado en él durante un período prolongado.
Para esta investigación, mi punto de partida lo proporciona la observación de que el producto
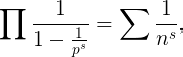
Si se sustituye a p con todos los números primos, y a n con todos los números enteros. Las funciones de variable compleja s que están representadas por estas dos expresiones, donde quiera que converjan, las denoto por ζ(s).
Ambas expresiones convergen solo cuando la parte real es mayor que 1; al mismo tiempo, se puede encontrar fácilmente una expresión para la función que siempre es válida. Al hacer uso de la ecuación
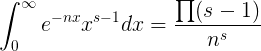
primero se ve que
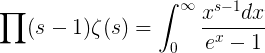
Si se considera ahora la integral
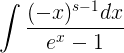
de +∞ a +∞ tomada en sentido positivo alrededor de un dominio que incluye el valor 0 pero no otro punto de discontinuidad del integrando en su interior, entonces se ve fácilmente que
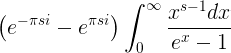
siempre que, en la función multi-valuada (−x)s−1 = e(s−1) ln(−x), el lo-garitmo de −x se determina de manera que sea real cuando x es negativo.
Por lo tanto
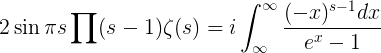
donde la integral tiene el significado que se acaba de especificar (nota del traductor: hoy en dia integral de contorno o linea).
Esta ecuación ahora proporciona el valor de la función ζ(s) para todos los números complejos s y muestra ademas que esta función tiene un unico valor y es finita para todos los valores finitos de s a excepción de 1, y también que es cero si es igual a un número entero par negativo.
Si la parte real de s es negativa, entonces, en lugar de tomarse en un sentido positivo alrededor del dominio especificado, esta integral también puede tomarse en un sentido negativo alrededor de ese dominio que contiene todas las cantidades complejas restantes, ya que la integral tomada con valores infinitamente grandes para el módulo, es infinitamente pequeña.
Sin embargo, en el interior de este dominio, el integrando tiene discontinuidades solo donde x se convierte en igual a un múltiplo entero de + − 2πi, y la integral es, por lo tanto, igual a la suma de las integrales tomadas en sentido negativo alrededor de estos valores.
Pero la integral alrededor del valor n2πi es = ((−n2πi)^(s−1))(−2πi), de lo que se obtiene

así, una relación entre ζ(s) y ζ(1−s), que, mediante el uso de propiedades conocidas de la función ∏, puede expresarse de la siguiente manera:
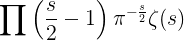
la cual, permanece sin cambios cuando se reemplaza por 1−s.
Esta propiedad de la función me indujo a introducir, en lugar de ∏(s−1), la integral ∏(s 2 −1) en el término general de la serie ∑ 1/n^s, por lo que se obtiene una expresión muy conveniente para la función ζ(s) .
De hecho

así, si uno establece
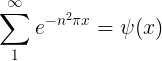
luego
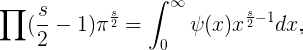
o desde
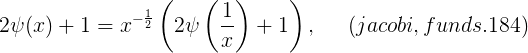
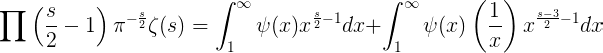
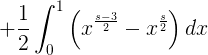
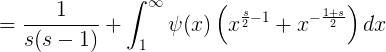
Ahora se define s = 1/2 + ti y
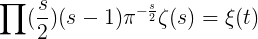
así que
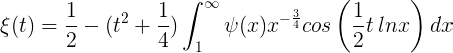
o, además,
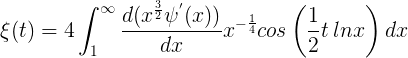
Esta función es finita para todos los valores finitos de t, y permite por si misma desarrollarse en potencias de t^2 como una serie que converge muy rápidamente. Dado que, para un valor de cuya parte real es mayor que 1, lnζ(s) = −∑ln(1−p^−s) permanece finito, y dado que lo mismo ocurre para los logaritmos de los otros factores de ξ(t), se deduce que La función ξ(t) solo puede desaparecer si la parte imaginaria se encuentra entre 1/2i y -1/2i.
El número de raíces de ξ(t) = 0, cuyas partes reales se encuentran entre 0 y T es aproximadamente
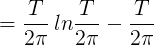
porque la integral ∫d lnξ(t), tomada en sentido positivo alrededor de la región que consiste en los valoresde t cuyas partes imaginarias se encuentran entre 1/2i y −1/2i y cuyas partes reales se encuentran entre 0 y T, es (hasta una fracción del orden de magnitud de la cantidad 1/T ) igual a(T ln T/2π −T)i; sin embargo, esta integral es igual al número de raíces de ξ(t) = 0 que se encuentran dentro de esta región, multiplicada por 2πi.
Se encuentra, de hecho, aproximadamente este número de raíces reales dentro de estos límites, y es muy probable que todas las raíces sean reales. Ciertamente, uno desearía una prueba más estricta aquí; Mientras tanto, dejé de lado temporalmente la búsqueda de esto después de algunos intentos fútiles fugaces, ya que parece innecesario para el próximo objetivo de mi investigación.
Si se denota por α todas las raíces de la ecuación ξ(α) = 0, se puede expresar lnξ(t) como
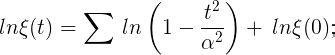
porque, dado que la densidad de las raíces de la cantidad t crece con t solo como ln t 2π, se deduce que esta expresión converge y se convierte para un t infinito solo infinta como t lnt; por lo tanto, difiere de lnξ(t) por una función de t^2, que para un t finito se mantiene continuo y finito y, cuando se divide por t^2, se vuelve infinitamente pequeño para un t infinito. En consecuencia, esta diferencia es una constante, cuyo valor se puede determinar mediante t = 0.
Con la ayuda de estos métodos, ahora se puede determinar el número de números primos que son más pequeños que x. Sea F(x) igual a este número cuando no es exactamente igual a un número primo; pero que sea mayor por un factor de 1/2 cuando x es un número primo, de modo que, para un x en el que hay un salto en el valor en F(x),
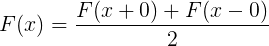
Si en la identidad

se reemplaza

Se obtiene
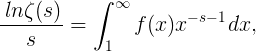
si uno denota
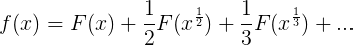
Esta ecuación es válida para cada valor complejo a + bi de s para el que a > 1.
Si, sin embargo, la ecuación
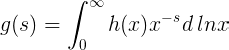
se mantiene dentro de este rango, entonces, haciendo uso del teorema de Fourier, uno puede expresar las funciones en términos de la función g. La ecuación se descompone, si h(x) es real y
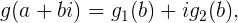
en los dos siguientes:
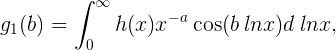
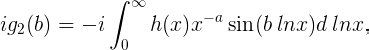
Si uno multiplica ambas ecuaciones por
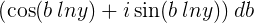
y las integra de −∞a +∞, luego se obtiene πh(y)y^−α en el lado derecho de ambos, debido a los teoremas de Fourier; por lo tanto, si se suman ambas ecuaciones y se multiplican por iy^α, se obtiene
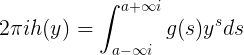
donde la integración se lleva a cabo de modo que la parte real de s permanece constante. Para un valor de y donde existe un salto en el valor de h(y), la integral toma el promedio de los valores de la función h en cada lado del salto. De la manera en que se definió la función, vemos que tiene la misma propiedad y, por lo tanto, en general

Se puede sustituir por lnζ la expresión
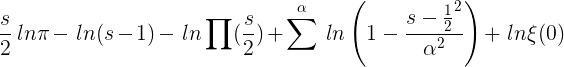
encontrado anteriormente; sin embargo, las integrales de los términos individuales de esta expresión no convergen, cuando se extienden al infinito, por lo que es apropiado convertir la ecuación anterior mediante la integración por partes en
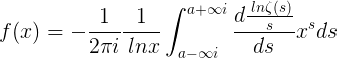
Ya que
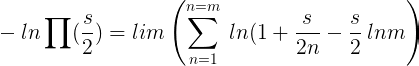
para m = ∞ y por lo tanto
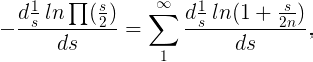
entonces se deduce que todos los términos de la expresión para f(x), con la excepción de
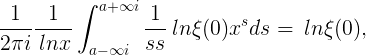
toman la forma
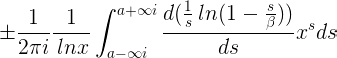
Pero ahora
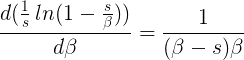
y, si la parte real es mayor que la parte real de β,

ó
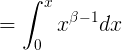
dependiendo de si la parte real de β es negativa o positiva. Uno tiene un resultado

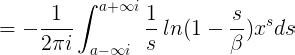
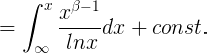
en el primero, y
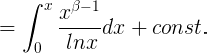
en el segundo caso.
En el primer caso, la constante de integración se determina si uno deja que parte de β se vuelva infinitamente negativa; en el segundo caso, la integral de 0 a x toma valores separados por 2πi, dependiendo de si la integración setoma através de valores complejos con argumento positivo o negativo, y se vuelve infinitamente pequeña, para la ruta anterior, cuando el coeficiente de i en el valor de β se vuelve infinitamente positivo, pero para este último, cuando este coeficiente se vuelve infinitamente negativo.
De esto se ve cómo en el lado izquierdo ln(1− s β) debe ser deteminado para que las constantes de integración desaparezcan. Mediante la inserción de estos valores en la expresión para f(x) se obtiene
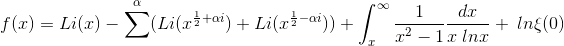
si en ∑^α se sustituye por α todas las raíces positivas (o raíces que tienen una parte real positiva) de la ecuación ξ(α) = 0, ordenadas por su magnitud.
Puede mostrarse fácilmente, mediante una discusión más exhaustiva de la función ξ, que con este orden de términos el valor de la serie
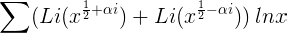
está de acuerdo con el valor límite al que
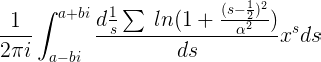
converge a medida que la cantidad aumenta sin límite; sin embargo, cuando se vuelve a ordenar, puede tomar cualquier valor real arbitrario. De f(x) se obtiene F(x) por inversión de la relación

para obtener la ecuación
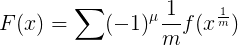
en el que uno sustituye a la serie que consiste en aquellos números naturales que no son divisibles por ningún cuadrado que no sea 1, y en el que µ denota el número de factores primos de m. Si uno restringe ∑α a un número finito de términos, entonces la derivada de la expresión para f(x) o, hasta una parte que disminuye muy rápidamente con el crecimiento de x,
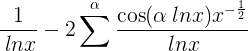
da una expresión aproximada para la densidad del número primo + la mitad de la densidad de los cuadrados de los números primos + un tercio de la densidad de los cubos de los números primos, etc. en la magnitud x. La expresión aproximada conocida F(x) = Li(x) es, por lo tanto, válida hasta cantidades del orden x^1/2 y da un valor algo demasiado grande; porque los términos no periódicos en la expresión para F(x) son, aparte de las cantidades que no crecen infinitas con x:
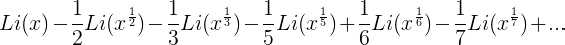
De hecho, en la comparación de Li(x) con el número de números primos menores que x, realizado por Gauss y Goldschmidt y llevado hasta x = tresmillones, este número ha demostrado ser, en los primeros cien mil, siempre menor que Li(x); de hecho, la diferencia crece, con muchas fluctuaciones, gradualmente con x.
Pero también el aumento y la disminución de la densidad de los números primos de un lugar a otro que depende de los términos periódicos ya ha llamado la atención, sin embargo, no se ha observado ninguna ley que rija este comportamiento.


