¿Qué es una función?
Una función es una relación que hay entre un conjunto de valores y otro. Ejemplo de función matemática:
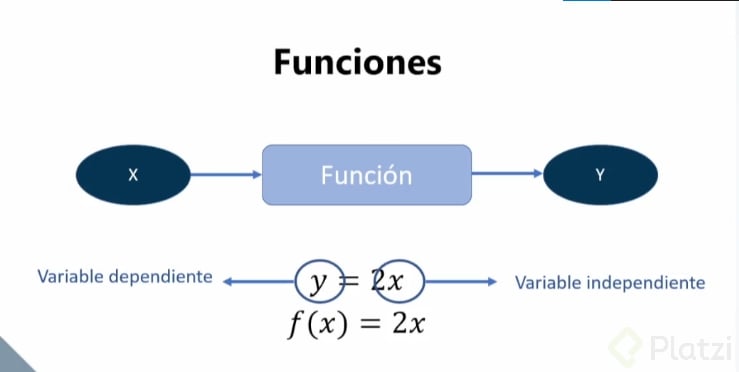
Si decimos que el valor de la temperatura del día depende de la hora a la que la consultemos, estaremos sin saberlo estableciendo entre ambas cosas una función. Ambas magnitudes son variables, pero se distinguen entre:
- Variable dependiente: Es la que depende del valor de la otra magnitud. En el caso del ejemplo, es la temperatura.
- Variable independiente: Es la que define la variable dependiente. En el caso del ejemplo es la hora.
En las funciones, los valores de y dependen de los valores ingresados por x.
¿Cómo escribir funciones?

Tabulación de funciones
Recordemos que en una función tenemos la variable independiente (x, qué es donde ingresan los datos) y la variable dependiente (y, qué son los valores arrojados luego de que se ingresó x). Entonces, con las funciones podemos hacer una tabla en dónde ingresamos valores para x, obteniendo resultados en y.
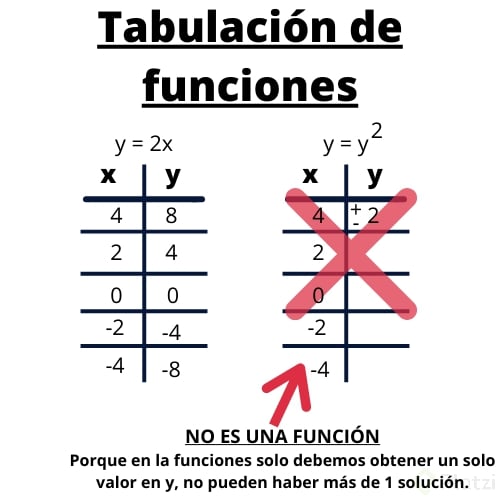
- SI POR UNA X OBTENEMOS DOS Y, ENTONCES NO ES FUNCIÓN. SOLO SE PUEDE TENER UN VALOR DE ENTRADA Y OTRO DE SALIDA.
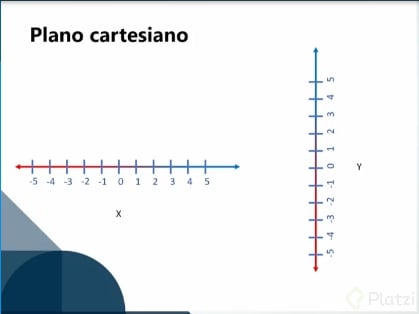
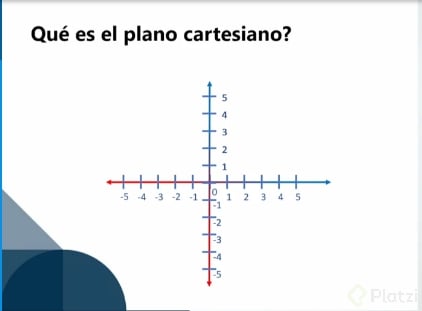
Plano cartesiano
¿Cómo graficar en el plano cartesiano?
- A la hora de ubicar una función, tenemos que tener en cuenta que cuando nos encontremos con cosas como (3, 4) significa que el primer número que está es X, mientras que el segundo es Y, por lo que 3 es X y 4 es Y.
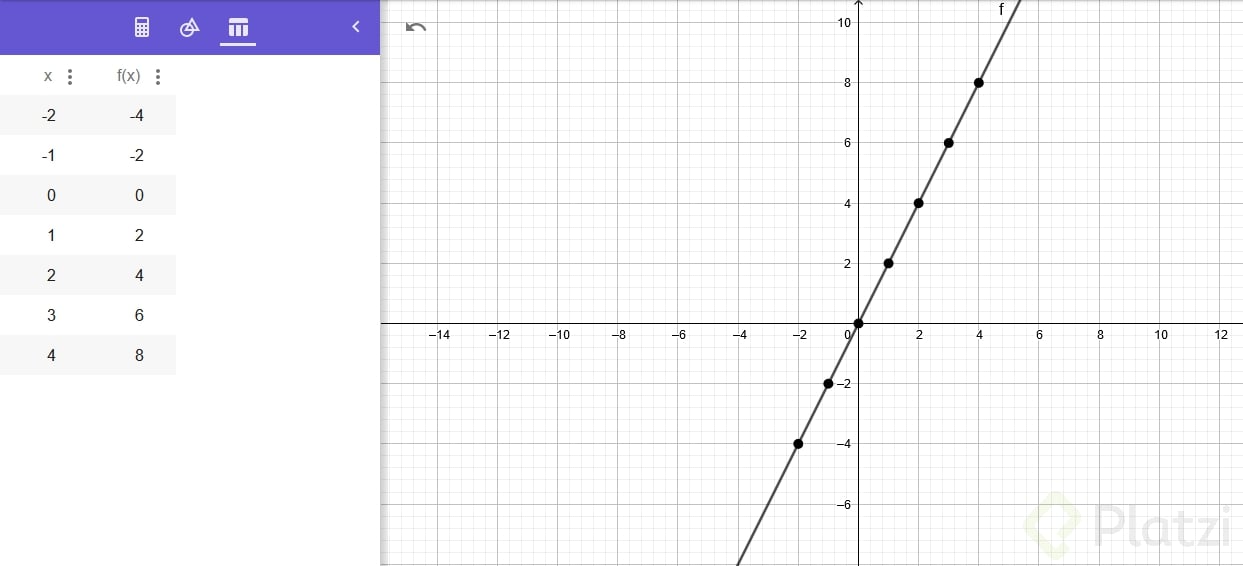
- Teniendo en cuenta esto, vamos con un ejemplo. Tenemos la función y = 2x junto a la tabla, por lo que podemos empezar a graficar los primeros puntos:

- Ahora, tras marcar todos los puntos, podemos trazar una línea que atraviese todos los puntos, formando una línea. Esto se conoce como función lineal:
Apuntes extra:
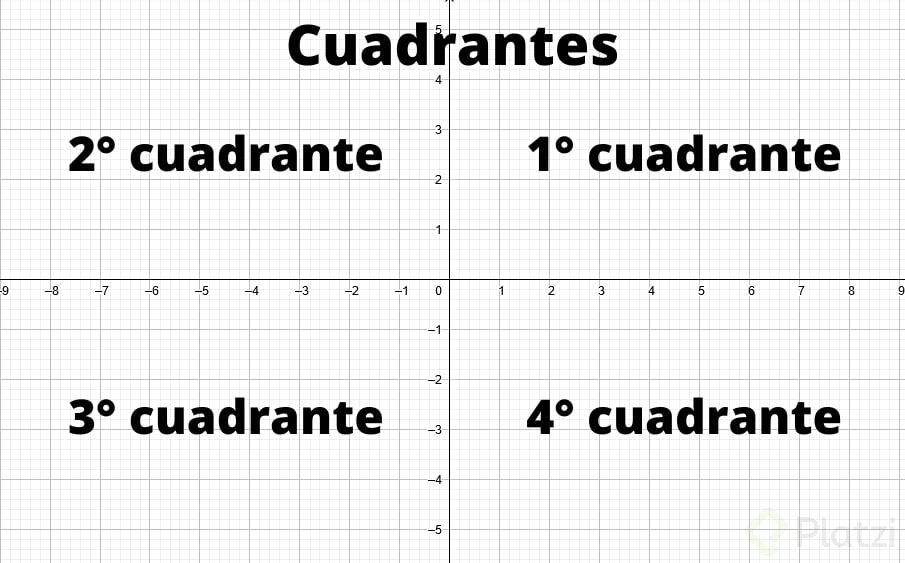
- Existe algo llamado cuadrantes, qué es lo que divide en 4 partes al plano cartesiano. Aquí tienes cada cuadrante por su orden correspondiente:
Funciones lineales y pendiente
-
Las funciones lineales las vamos a utilizar y ver de forma frecuente en nuestra vida cotidiana, estas funciones básicamente son líneas y su fórmula y = mx en donde m se llama pendiente. La pendiente nos sirve para ver qué tan rápido crece o decrece nuestros valores de la función.
-
Mientras más grande sea el valor de la pendiente más se va a acercar a la línea vertical, pero nunca la va a tocar. Por otro lado, si nuestra pendiente tiene un valor menor a 1 y mayor a 0, se irá acercando a la línea horizontal del plano cartesiano. Es muy sencillo saber cuando la línea tocará el eje X, es cuando la pendiente vale 0, por lo que no tiene inclinación.
-
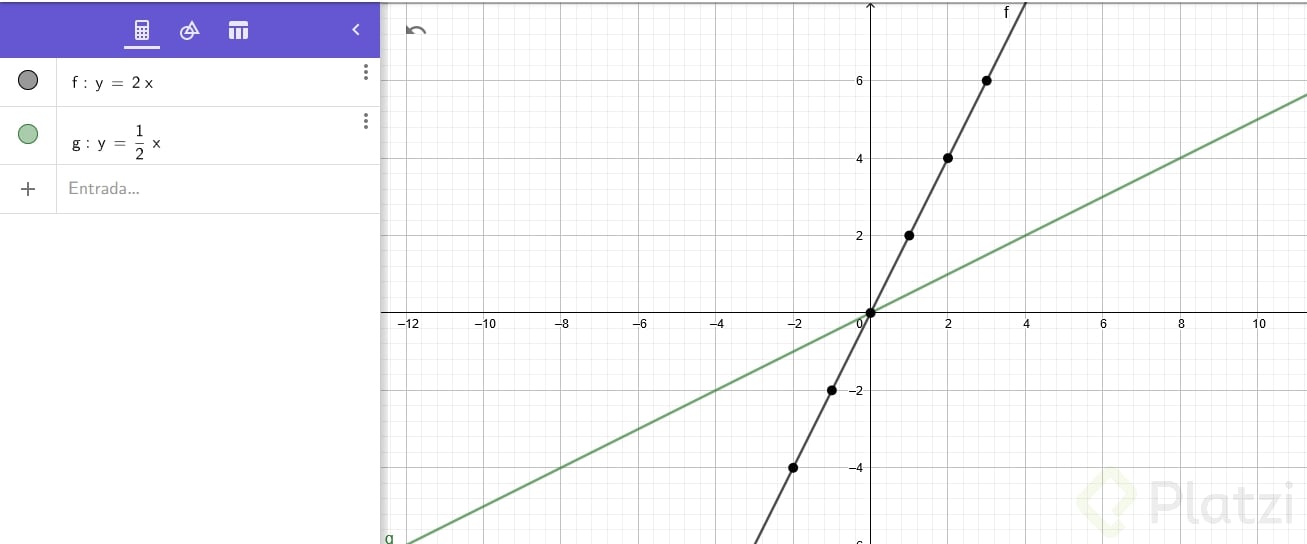
Mira este ejemplo, acá podemos ver qué tenemos 2 funciones con pendientes distintas, en donde la linea negra tiene una pendiente más alta, y la linea verde tiene una pendiente mucho menor.
-
Recordar:
- m>0 la función crece
- m<0 la función decrece
-
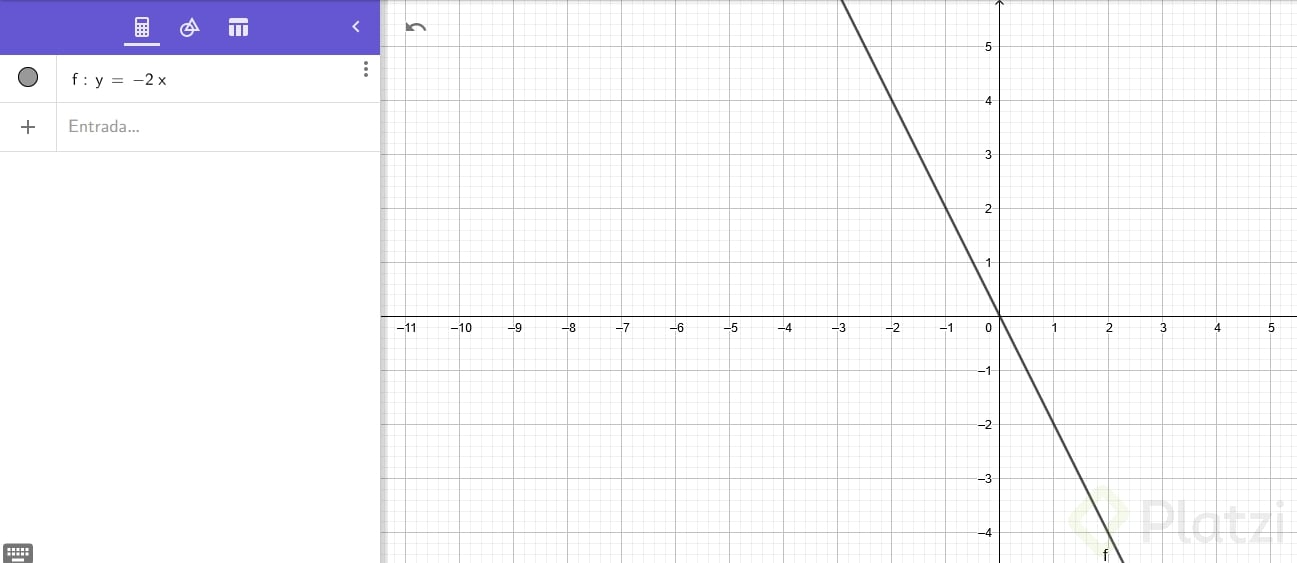
Si queremos que la pendiente esté dirigida hacia los cuadrantes de la izquierda (cuadrante 2 y 3), entonces lo que debemos hacer en la fórmula de la función agregarle un -a la pendiente, o sea, hacer que la pendiente sea negativa. Mira este ejempl, en dónde vas a ver que la función indica que la pendiente es -2, por lo tanto es negativa.
:
-
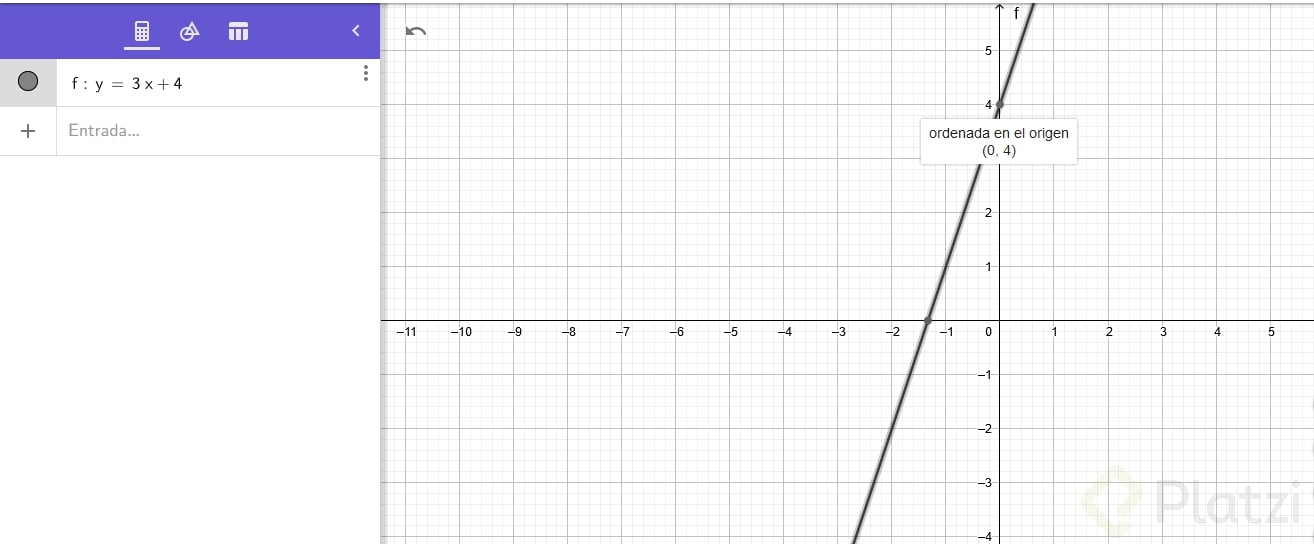
¿Y cómo hacemos para que nuestra función no corte en el eje 0, sino que queremos que la ordenada al origen sea por ejemplo 4? Sencillo, debemos utilizar ahora la siguiente fórmula: y = mx +/- b. En esta función agregamos a B, qué es la ordenada al origen, o sea el punto en donde corta Y. Mira este ejemplo para entenderlo mejor, en dónde en la función aclaramos que B sea igual 4:
Identificar funciones lineales a partir de sus ecuaciones
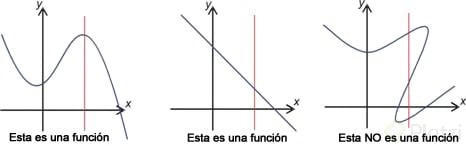
- Las funciones no se encuentran siempre en ecuaciones ordenadas al igual que su fórmula correspondiente, como por ejemplo con la funciones lineales.
- Identificar si una función no es lineal a partir de su ecuación es bastante fácil, si la ecuación tiene algún exponente al cuadrado entonces ya no es una función lineal.

Tipos de funciones por su ecuación
Agradezco estas imágenes a el compañero en Platzi @fabiolavcj por sus aportes a través de las imágenes, acá te dejo sus links para que vayas a verlos:
-
Primer aporte: https://platzi.com/comentario/1384589/
-
Segundo aporte: https://platzi.com/comentario/1384566/
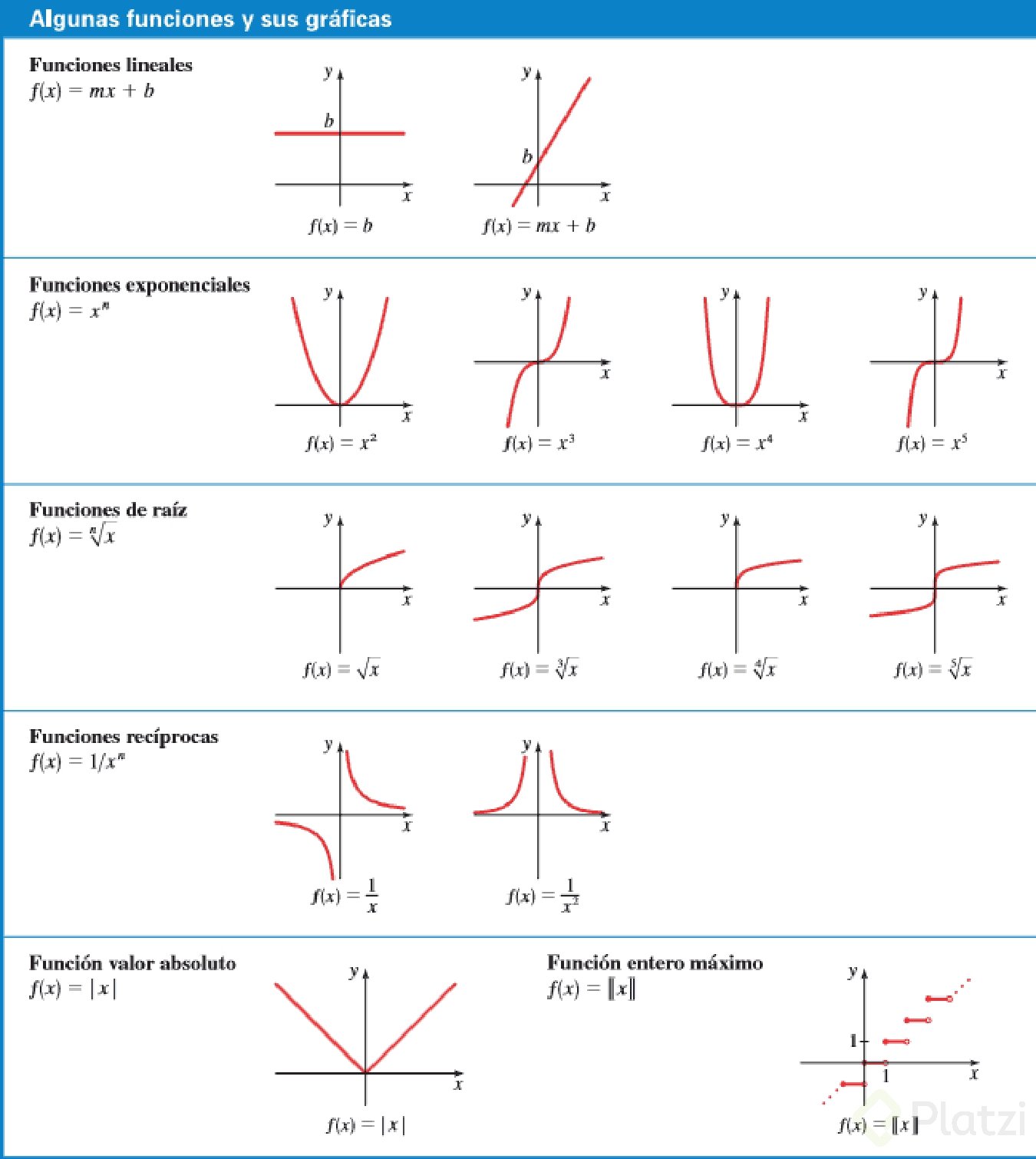
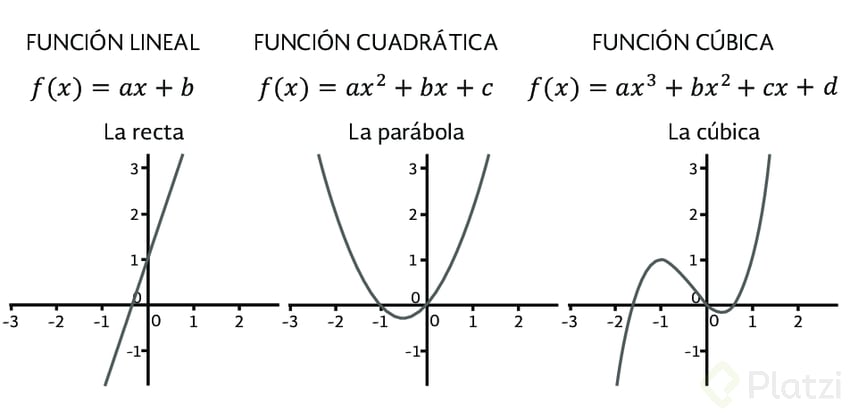
Curso de Fundamentos de Matemáticas
COMPARTE ESTE ARTÍCULO Y MUESTRA LO QUE APRENDISTE