Si te costo trabajo entender el metodo de Principal Component Analysis,encontre una forma de entenderlo de forma intuitiva, el unico requisito es que hayas hecho la clase de Autovalores y Autovectores y que sepas que es la varianza, que es algo que se explico en el curso de estadistica.
Para iniciar recordemos que este algoritmo es usado para reducir la dimension de nuestro dataset, es decir, si tengo tres dimensiones, con PCA lo reducire todo a 2 dimensiones, nuestra dimension tiene que ser mayor o igual a 2 ya que si tenemos una dimension no podemos reducirlo mas.
1-Empezemos con nuestro dataset, es importante identificar su dimension y para ello tenemos que identificar cuantos features tenemos, por ejemplo tengo como feature el peso(xi) de un grupo de personas, y los usare para predecir su edad(yi), por ende tenemos una dimension 2D.Luego como se vio en la clase al inicio, el profesor estandarizo los datos, es decir, les resto a cada uno el promedio o mean, debemos hacer esto tambien.
xi = xi - mean(xi)
yi = yi-mean(yi)
2-Hallamos la covarianza de nuestros datos con esta formula:
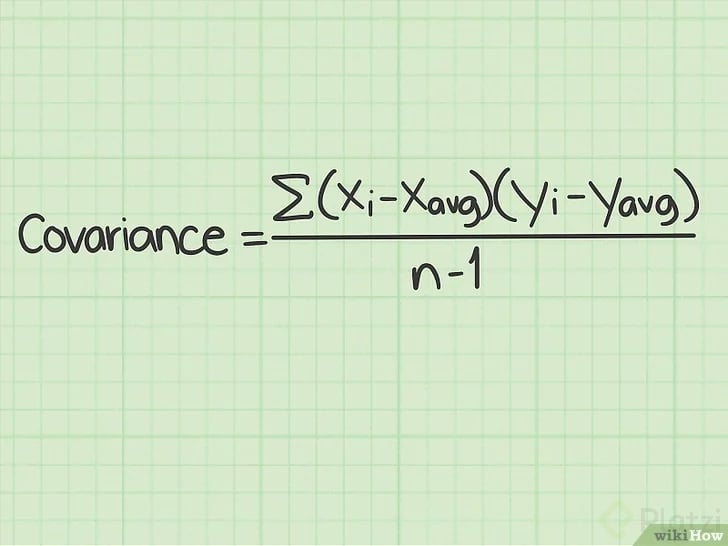
Podemos ver que esta formula no es mas que la sumatoria de la multiplicacion de la resta de nuestro dataset(xi,yi) menos el promedio, entre el numero de datos menos uno
3- Ahora que sabemos cual es la covarianza, sacamos la varianza y hallamos nuestra matriz de covarianza:
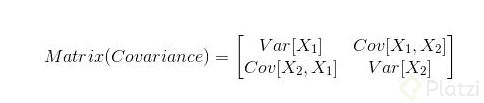
4-Como ya viste la clase de Eigenvectors y Eigenvalues, lo que sigue ahora es que a la matriz de covarianza le sacamos justamente eso, los autovalores y autovectores, para que podamos obtenerlos se debe cumplir esta formula:
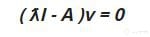
Donde lambda son los autovalores y v los autovectores, ademas si tenemos una matriz de orden n, obtendremos
n autovalores y n autovectores, es decir tenemos 2 autovectores(cada uno con una dimension de 2x1), insisto, si aca te perdiste toma la clase de autovalores y autovectores
5-Seleccionamos los autovectores a los que les corresponda los autovalores mas altos, en este caso solo podemos tomar uno, ya que tenemos dos autovectores
6-Hallamos nuestros Principal Components con esta formula:

Donde FeatureVector^T es la transpuesta del autovector(paso 4) que seleccionamos y ScaledData^T es la transpuesta de la matriz de nuestros features estandarizados(paso 1).
Como nuestro autovector tiene la forma 2x1 y nuestro dataset tienen la forma nx2, al sacar la transpuesta tenemos una matriz de 1x2 por una matriz de 2xn, donde vemos que si se pueden multiplicar, ya que la primera tiene 2 columnas y la segunda 2 filas, ahora para saber la dimension del producto, tomamos las filas de la primera matriz con las columnas de la segunda,es decir nuestro resultado es de 1xn, lo que quiere decir que todo lo reducimos a una dimension.
Listo, con esto obtenemos nuestros Principal Components, de tener un espacio bidimensional, pasamos a tener un subespacio de dimension 1, a fin de cuentas, una linea recta:
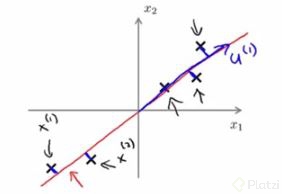
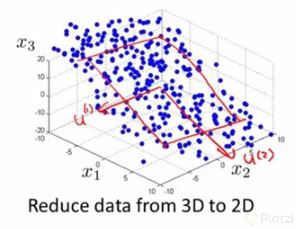
Este mismo proceso se puede usar para multiples dimensiones, el objetivo es obtener un hiperplano, es decir un subespacio de menor dimension que abarque la mayor cantidad de datos.Por ejemplo en un espacio de dimension 3, al hacer PCA lo que se hace es obtener un hiperplano 2D:
Creditos: Andrew Ng