¿Por qué obtengo resultados inesperados con los float? 🤔 ¿Comó lidiar con eso? 🔧

Seguro conocerás los números de punto flotante ¿Verdad? pero, ¿Me puedes decir que retornará la siguiente expresión en la consola de Python?

>>> (0.1 + 0.1 + 0.1) == 0.3

Tal vez no lo parezca, pero esa expresión devuelve False

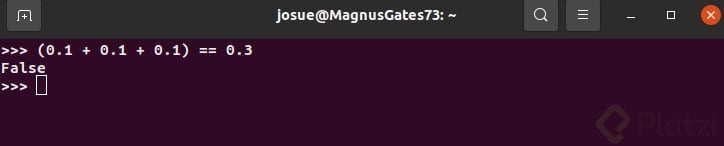
¿Porque pasa exactamente esto?

Aquí te explico porqué y como lidiar con esto 👨‍🔧

Sistemas de numeración decimal y binario

Para empezar entendamos como es que representamos los números.

Un sistema de numeración es un conjunto de reglas para expresar cantidades válidas. Ambos el sistema Decimal y Binario cuentan con un número determinado de digitos, a eso se le llama base.

Sistema Decimal
Base 10 (0,1,2,3,4,5,6,7,8,9)

Sistema Binario
Base 2 (0,1)

Los dos son sistemas posicionales, eso quiere decir que el valor de un digito en una cantidad expresada depende de la posición en la que se encuentre.

Para expresar números enteros en ambos sistemas esas posiciones comienzan desde la derecha y van hacia la izquierda desde la posición 0 y pueden terminar en la posición infinito.
La manera de calcular el valor del digito en un número expresado es la siguiente:

digito x (base^posición)

y el valor total de la cantidad expresada es igual a la suma del valor de cada digito.
Veamos un ejemplo en ambos sistemas.

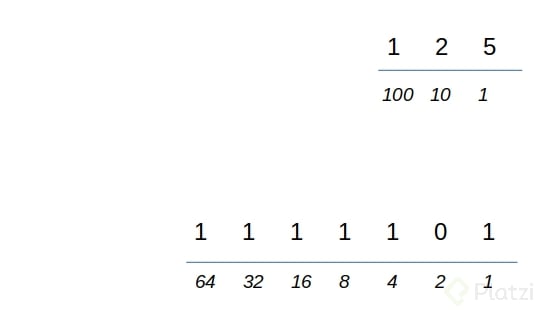
Los 2 sistemas representan la cantidad 125.
Los números por encima de la linea son los digitos y los números debajo de la linea son las potencias de su respectiva base. Quizá te llame la atención el 1 que aparece al inicio pero recuerda que comenzamos desde la posición 0 y cualquier número a la 0 es 1

10^0 = 1
2^0 = 1

Ahora calculemos el valor total en cada sistema:

(1 x 100 + 2 x 10 + 5 x 1) = 125
(1 x 64 + 1 x 32 + 1 x 16 + 1 x 8 + 1 x 4 + 0 x 2 + 1 x 1 ) = 125

Números decimales

Todo bien con los números enteros, pero ¿como expresamos los numeros que no lo son?. De la misma manera que en los números enteros, los decimales se expresan con digitos en diferentes posiciones pero esta vez van de izquierda a derecha, además no tenemos ese 1 al principio dado que esta en el lado de los enteros.
Imagina la recta de números positivos y negativos, así es como la notación científica se usa para expresar números muy grandes o muy pequeños:

23x10^46 (un número bastante grande)
ó
3.8x10^-15 (un número muy pequeño)

Veamos un ejemplo de como expresariamos un decimal en ambos sistemas:

De nuevo tenemos los digitos en la parte superior de la linea y las potencias de la base debajo. En este caso el valor del digito se calcula dividiendo, tiene sentido ¿no?, la operación inversa a la que utilizamos con los enteros ¿cierto?.
Bueno lo que en realidad pasa es esto:

1 x 10^-1 es equivalente a 1 x (1/10^1) que a su vez es equivalente a (1/1) x (1/10^1)

y tu ya sabes multiplicar fracciones, ¿verdad?

Entonces para efectos prácticos solo dividamos el digito entre la potencia de la base:

Sistema Decimal
1/10 + 2/100 + 5/1000 = .125

Sistema Binario
0/2 + 0/4 + 1/8 = .125

Entonces, ¿Cúal es el problema?

Ya vimos como los humanos representamos números de punto flotante y como lo hacen las computadoras sin embargo; hay algunos números bastante largos, muuuuuuuuy largos. Por ejemplo:

1/3

Los humanos podríamos representar esa fracción así

0.3

o aún mejor

0.33

inclusive mucho mejor

0.333

El dilema con este tipo de números es que no importa cuantos digitos mas agreguemos, jamás sera exactamente 1/3, se acercá, pero no lo es. Lo mismo sucede en binario, por ejemplo con el número 1/10

.0001100110011001100110011001100110011001100110011…

Te reto a que calcules el valor de cada bit, los sumes (ya sabes como hacerlo) y revises por ti mismo si ese binario es exactamente 0.1 ó puedes usar este script que escribí en Python 3.9

defbinary(binary_num):
    sums = 0.0
    pos = 1
    for i in binary_num:
        if i == '1':
            sums += round(1/(2**pos),10)
        pos += 1
    return round(sums, 10)

defmain():
    #ingresa solo los bits despues del punto y sin los tres puntos finales
    bin_num = input('Give me the binary num: ')
    result = binary(bin_num)
    print(f'{bin_num} is {result} in decimal')

if __name__ == '__main__':
    main()

La memoria

La memoria juega un papel crucial en la representación de números de punto flotante pues en la mayoria de computadoras Python utiliza 53 bits para representarlos, esto es una limitante ya que hay números que ni 53 digitos bastan para representarlos exactamente.
La aproximación mas cercana será guardada y Python te mostrará el valor redondeado, ¡pero eso no significa que ese sea el número que esta guardado en la computadora!

Es por eso que:

(0.1 + 0.1 + 0.1 == 0.3) retorna False

Solución

Relajate, esto no quiere decir que ya no puedes confiar en los números de punto flotante

El que haya inexactitudes a la hora de representarlos no es un bug en Python, ni tampoco hay nada mal en tu código, esto es propio de la naturaleza de los binarios a la hora de guardar flotantes y pasa en muchos otros lenguajes. Lo importante es que entiendas que la aritmetica que se lleva acabo en las computadoras es binaria, no decimal.
Si bien hay algunas inexactitudes, estas son muy poquisimas y en la mayoria de cálculos comunes obtendrás lo que esperas si redondeas los resultados finales

esto le dirá a Python que solo considere una parte del número y no todo lo que esta guardado.

Si lo que necesitas son representaciones precisas de numeros decimales utiliza el modulo decimal en Python
👉 https://docs.python.org/3/library/decimal.html#module-decimal

Tambien existe el modulo fractions para representar exactamente fracciones
👉 https://docs.python.org/3/library/fractions.html#module-fractions