Algoritmos de ordenamiento

Los algoritmos de ordenamiento han sido fuente de gran interés e investigación desde el inicio de la computación, aunque su resolución es relativamente simple a lo largo de la historia se ha diseñado numerosas técnicas para lograr el algoritmo más eficiente que logre ordenar una lista de la manera más rápida y eficiente.

La gran variedad y cantidad de algoritmos de ordenamiento diferentes los hace un buen tema para el aprendizaje de cualquier lenguaje de programación. Para programar uno de estos algoritmos es necesario aplicar conceptos de arreglos, operaciones de comparación y operaciones aritméticas.

A continuación se listan algunas de las características por las cuales pueden clasificarse los algoritmos de búsqueda

COMPLEJIDAD COMPUTACIONAL
La complejidad computacional es el mejor, promedio y peor comportamiento que tiene un determinado algoritmo dependiendo del tamaño de la lista. La cantidad de pasos a realizar dependerá en muchos casos del nivel de desorden inicial de la lista, por lo que son necesarios estos tres valores para comparar el rendimiento de los diferentes algoritmos.

Para describir la complejidad computacional de un algoritmo de ordenamiento para una lista de tamaño n se utiliza la notación O() que indica la cantidad de operaciones necesarias para finalizar el algoritmo correctamente. Por ejemplo O(n) significa que el algoritmo necesita tantos pasos como elementos en la lista para finalizar.

USO DE MEMORIA
Aunque la mayoría de los algoritmos no utilizan más memoria que un espacio extra que el ocupado por la lista a ordenar algunos requieren espacio adicional.

Aquellos algoritmos que solo requieren un espacio adicional de memoria o O(1) son denominados algoritmos in situ o in-place. Una definición más amplia de este término incluye también aquellos que ocupan una memoria igual a O(log(n))

ESTABILIDAD
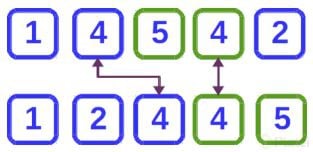
Cuando los elementos de la lista a ordenar tienen varias características pero solo se utiliza una de ellas para ordenar pueden darse dos tipos de ordenamiento dependiendo del algoritmo. En el siguiente ejemplo se ve una lista de números que pueden tener color azul o verde. La lista se ordenará por número y en este caso particular el número 4 se encuentra dos veces con diferente color.

En este caso el algoritmo mantiene el orden relativo que tenia la lista original colocando el 4 azul primero que el 4 verde. A esto se le llama un algoritmo estable.

En este otro caso, en cambio, al ordenar es posible que el orden relativo se modifique quedando el 4 verde primero que el 4 azul. A esto se le llama algoritmo inestable.

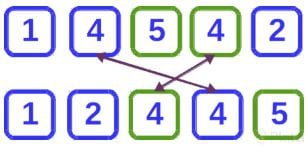
La estabilidad de el algoritmo de ordenamiento tendrá relevancia dependiendo de la naturaleza de la lista, en el caso de que la lista tenga una sola característica o que no existan elementos con la misma característica entonces el resultado de un algoritmo estable no variará que el de uno inestable.

METODO
El método es el proceso elegido para lograr el ordenamiento de la lista, entre ellos puede nombrarse

• Inserción,
• Intercambio,
• Selección
• Unión
• Particionado.

SERIAL/PARALELO
Aunque la mayoría de los algoritmos presentados estén diseñados para operaciones en serie existen otros que aprovechan las ventajas de el procesamiento paralelo. Estos permiten realizar operaciones en paralelo sobre la lista permitiendo reducir el tiempo requerido.

COMPARATIVOS/NO COMPARATIVOS
Se les llama algoritmos comparativos a aquellos que comparan de dos elementos a la vez utilizando un operador de comparación. Otros tipos de algoritmos como los de ordenamiento entero utiliza operaciones aritméticas sobre las claves para obtener el ordenamiento.