Al igual que a otros de mis compañeros, la sección de concurrencia en Go me pareció deficiente, así que decidí hacer este tutorial para complementar el conocimiento, además me gustaría hacer un llamado al team de QA de los cursos de platzi para que revisen el contenido y los comentarios de las clases para mejorarlas.
En fin, en este tutorial veremos primero una corrección al código de fibonacci mostrado en clase, después veremos el algoritmo de Gauss-Jordan con y sin manejo de concurrencia, y su comparativa.
<h1>Fibonacci</h1>En la clase se crea una cache para valores más “externos”, o sea se guarda en cache el 42, 40, 41, 38. Lo cual no es eficiente pues el algoritmo sigue siendo factorial, ve la siguiente imagen
Observa cómo se repiten muchas llamadas a fib. Lo que haría el código de la clase sería calcular todas esas llamadas, y luego guardar en cache el valor de fib(5). Ahora, piensa en lo que haría el código si se llamara a fib(42), el árbol de recursión sería muy grande, pero por fortuna ya tenemos el valor de fib(5) en memoria, ¿pero qué hay de todos los otros valores mayores a 5? Esos no están en memoria y hay que computarlos, el algoritmo es en extremo ineficiente (para que veas esto más claro, haz a mano el árbol de recursión de fib(42) pero no incluyas fib(5) porque ya está en cache).
Una solución a esto es almacenar en cache no solo los valores “externos” sino todos, y eso lo hace el siguiente código.
package main
import (
"time""fmt"
)
func Fibonacci(n int, cache map[int]int64) int64 {
if n <= 1 {
returnint64(n)
}
var prev int64if c, exists := cache[n - 1]; exists {
prev = c
} else {
prev = Fibonacci(n - 1, cache)
cache[n - 1] = prev
}
var prevPrev int64if c, exists := cache[n - 2]; exists {
prevPrev = c
} else {
prevPrev = Fibonacci(n - 2, cache)
cache[n - 2] = prevPrev
}
return prev + prevPrev
}
func main() {
var numbers []int = []int{42, 40, 41, 42, 38}
var cache map[int]int64 = make(map[int]int64)
for _, n := range numbers {
start := time.Now()
fib := Fibonacci(n, cache)
fmt.Printf("fibonacci(%d) = %d (took %s)\n", n, fib, time.Since(start))
}
// look at cache contents and compare it with the other code
fmt.Println(cache)
}
Si ejecutamos el código veremos una mejor muy significativa en los tiempos que tarda el programa.
fibonacci(42) = 267914296 (took46.887µs)
fibonacci(40) = 102334155 (took294ns)
fibonacci(41) = 165580141 (took190ns)
fibonacci(42) = 267914296 (took163ns)
fibonacci(38) = 39088169 (took189ns)
Algo muy similar se puede hacer también para calcular factoriales.
<h1>Gauss-Jordan</h1>La implementación anterior de fibonacci no tiene mucho que ver con concurrencia, y claro, podríamos meter varias go routines, locks y demás, pero no me parece que eso muestre claramente la ventaja de usar concurrencia a no usarla. Por ello, propongo otro ejemplo: El algoritmo de Gauss-Jordan para reducir una matriz a su forma escalonada reducida.
(Si no conoces el algoritmo checa algún curso aquí mismo en platzi o en internet, si te sirve yo hice una página para visualizar el algoritmo paso a paso https://linalg.benjaminguzman.net)
package main
import (
"fmt""math/rand""strings""sync""time"
)
type RowReducer struct {
nRows uint
nCols uint
mat [][]float64
}
func NewRowReducer(nRows uint, nCols uint) *RowReducer {
var reducer RowReducer = RowReducer{nRows, nCols, make([][]float64, nRows)}
// allocate all rows in a single slice and partition that slice into columns to form rows// this is more efficient than allocating n rowsvar rows []float64 = make([]float64, nRows * nCols)
for i := uint(0); i < nRows; i++ {
reducer.mat[i] = rows[i * nCols:(i + 1) * nCols]
}
return &reducer
}
// fill the matrix with random values// returns the same RowReducer objectfunc (r *RowReducer) Fill() *RowReducer {
for i := uint(0); i < r.nRows; i++ {
for j := uint(0); j < r.nCols; j++ {
r.mat[i][j] = rand.Float64() * 10
}
}
return r
}
func (r *RowReducer) String() string {
var builder strings.Builder
builder.Grow(int(r.nRows * r.nCols * 10))
builder.WriteString(fmt.Sprintf("%d x %d matrix\n", r.nRows, r.nCols))
for i := uint(0); i < r.nRows; i++ {
for j := uint(0); j < r.nCols; j++ {
builder.WriteString(fmt.Sprintf("%.6f ", r.mat[i][j]))
}
builder.WriteString("\n")
}
return builder.String()
}
// Sequential row reducefunc (r *RowReducer) Reduce(rref bool) *RowReducer {
var minDim uint = r.minDim()
for j := uint(0); j < minDim; j++ {
r.reduce(j, rref)
}
return r
}
// Row reduce with go routines and waitgroupfunc (r *RowReducer) ConcurrentReduce(rref bool) *RowReducer {
var wg sync.WaitGroup
var minDim uint = r.minDim()
for j := uint(0); j < minDim; j++ {
r.concurrentReduce(j, rref, &wg)
}
return r
}
func (r *RowReducer) minDim() uint {
var min uint = r.nCols // if only go had ternary operator...if r.nRows < r.nCols {
min = r.nRows
}
return min
}
// Perform elementary operation Matrix[row] - factor * Matrix[pivotRow] on the matrix// factor is determined in such way that Matrix[row][pivotCol] is 0func (r *RowReducer) reduceRow(row uint, pivotRow uint, pivotCol uint) {
if r.mat[row][pivotCol] == 0 {
return
}
var factor float64 = r.mat[row][pivotCol] / r.mat[pivotRow][pivotCol]
for j := pivotCol; j < r.nCols; j++ { // perform elementary operation Ri - factor * Rp
r.mat[row][j] -= factor * r.mat[pivotRow][j]
}
}
// col: the column to be reduced. When this method ends this column will have only 0's and at most one 1 // rref: if true matrix will be row reduced to the echelon form (Gauss-Jordan). If false, matrix will be reduced to the an upper triangular form (Gauss)func (r *RowReducer) reduce(col uint, rref bool) {
if col > r.nRows { // there are no rows to reducereturn
}
// select the pivot (first non 0 value in the column)for i := col; i < r.nRows; i++ {
if r.mat[i][col] != 0 {
// pivot row is i, swap it with the col row (the row at index col)
r.mat[col], r.mat[i] = r.mat[i], r.mat[col]
break
}
}
var pivotCol uint = col
var pivotRow uint = col // just for legibilityif r.mat[pivotRow][pivotCol] == 0 { //the column has 0 non-0 values, so it is already reducedreturn
}
// reduce rows above the pivotif rref {
for i := uint(0); i < pivotRow; i++ {
r.reduceRow(i, pivotRow, pivotCol)
}
}
// reduce rows below the pivotfor i := uint(pivotRow + 1); i < r.nRows; i++ {
r.reduceRow(i, pivotRow, pivotCol)
}
// make the pivot 1if pivot := r.mat[pivotRow][pivotCol]; pivot != 1 {
for j := pivotCol; j < r.nCols; j++ {
r.mat[pivotRow][j] /= pivot
}
}
// fmt.Println("After reduction", r)
}
func (r *RowReducer) concurrentReduce(col uint, rref bool, wg *sync.WaitGroup) {
if col > r.nRows { // there are no rows to reducereturn
}
// select the pivot (first non 0 value in the column)for i := col; i < r.nRows; i++ {
if r.mat[i][col] != 0 {
// pivot row is i, swap it with the col row (the row at index col)
r.mat[col], r.mat[i] = r.mat[i], r.mat[col]
break
}
}
var pivotCol uint = col
var pivotRow uint = col // just for legibilityif r.mat[pivotRow][pivotCol] == 0 { //the column has 0 non-0 values, so it is already reducedreturn
}
var reduceRow = func(idx uint) {
defer wg.Done()
r.reduceRow(idx, pivotRow, pivotCol)
}
// reduce rows above the pivotif rref {
wg.Add(int(pivotRow))
for i := uint(0); i < pivotRow; i++ {
go reduceRow(i)
}
}
// reduce rows below the pivot
wg.Add(int(r.nRows - pivotRow - 1))
for i := uint(pivotRow + 1); i < r.nRows; i++ {
go reduceRow(i)
}
// make the pivot 1if pivot := r.mat[pivotRow][pivotCol]; pivot != 1 {
for j := pivotCol; j < r.nCols; j++ {
r.mat[pivotRow][j] /= pivot
}
}
wg.Wait()
//fmt.Println("After reduction", r)
}
func measure(n uint) (time.Duration, time.Duration) {
var r1 *RowReducer = NewRowReducer(n, n).Fill()
var r2 *RowReducer = NewRowReducer(n, n).Fill()
startSeq := time.Now()
r1.Reduce(true)
elapsedSeq := time.Since(startSeq)
startConc := time.Now()
r2.ConcurrentReduce(true)
elapsedConc := time.Since(startConc)
return elapsedSeq, elapsedConc
}
func mean(arr []time.Duration) time.Duration {
var sum int64for _, d := range arr {
sum += d.Nanoseconds() //🤞 there is no overflow
}
var d time.Duration = time.Duration(sum / int64(len(arr))) * time.Nanosecond
return d
}
func main() {
const MAX_N uint = 1000//5000const STEP uint = 5const N_TESTS uint = 5var testResultsSeq [N_TESTS]time.Duration
var testResultsConc [N_TESTS]time.Duration
for n := STEP; n <= MAX_N; n += STEP {
//fmt.Printf("Measuring performance of %d tests with matrix size %dx%d...\n", N_TESTS, n, n)for t := uint(0); t < N_TESTS; t++ {
testResultsSeq[t], testResultsConc[t] = measure(n)
}
//fmt.Println("Sequential results:", testResultsSeq)//fmt.Println("Concurrent results:", testResultsConc)//fmt.Println()
fmt.Printf("%d,%d,%d\n", n, mean(testResultsSeq[:]).Milliseconds(), mean(testResultsConc[:]).Milliseconds())
}
//fmt.Println("Sequential", testResultsSeq)//fmt.Println("Concurrent", testResultsConc)//fmt.Println(reducer.Reduce(true))//fmt.Println(reducer.ConcurrentReduce(true))
}
Como verás, el código hace la reducción de la matriz tanto de forma secuencial como concurrente. Algo interesante a notar es que para el código concurrente no hay locks y no se limitan las goroutines activas.
El que no se limiten las goroutines activas fue por simpleza del programa, para no escribir tanto código.
El que no haya locks es porque no son necesarios, y esto es gracias a que cada goroutine trabaja con una sola fila al momento de reducir la matriz. Veamos un ejemplo, si tenemos una matriz de nxm dimensiones, y digamos que nuestro pivote está en la fila i, entonces tendremos n-i goroutines trabajando en las n-i filas debajo del pivote, cada una se encarga de una sola fila, no modifica otra fila que no sea la suya, y así no hay problemas de concurrencia. Además tendremos i-1 goroutines trabajando en las i-1 filas arriba del pivote, bajo el mismo esquema, cada una con su propia fila a trabajar.
Ahora, algo importante a notar es que a pesar que cada goroutine tiene su fila en específico, todas van a leer de la fila i, la fila del pivote, pero eso tampoco trae problemas porque la operación es de solo lectura, y además no hacemos ninguna operación de escritura durante el tiempo que estas goroutines se ejecutan, entonces es seguro. Nótese, que sí hay escritura en la fila del pivote, pero eso sucede hasta que todas las goroutines terminan su ejecución.
Aunque… técnicamente sí podría traer problemas porque supongamos que las goroutines se ejecutan en diferentes cores del procesador, entonces cada core tendría que tener una copia actualizada de los valores en la fila del pivote, sino los cálculos estarían mal, por lo que habría que actualizar la cache de los todos los cores antes de ejecutar las goroutines, de esta forma sabemos que van a leer datos actualizados. Algunos lenguajes permiten esta actualización entre los cores con keywords como volatile en el caso de java. Para go no sé cómo se haga eso, pero intuyo que lo hace automáticamente, y respecto a eso encontré este post muy interesante (está en inglés).
En la siguiente imagen se observa cómo agregar concurrencia mejora los tiempos de ejecución. Sin embargo, nótese que el comportamiento asintótico es el mismo.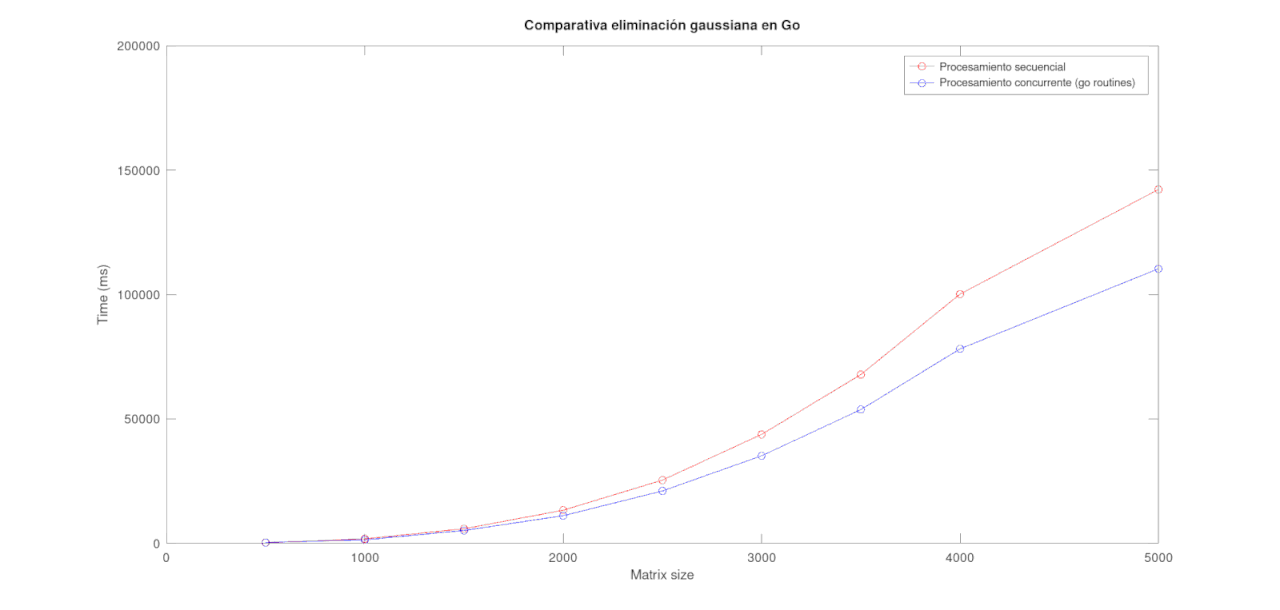
Asimismo, hay que notar que al usar concurrencia se agrega un pequeño overhead al programa, y en ocasiones este overhead es más que lo que se gana al usar concurrencia. En el gráfico a continuación se observa que la solución concurrente es menos eficiente que la secuencial para matrices “pequeñas”, seguramente debido a este overhead de inicializar las goroutines y otras cosas que tenga que hacer go para correrlo de forma concurrente.
