Imagina que tienes un set de 5 datos bidimensionales, es decir, tienes 5 coordenadas (x y y). Todos estos datos son datos reales que son tomados de mediciones. Ahora, tú quieres entender el comportamiento y tendencia de estos 5 datos para, por ejemplo, predecir el sexto, séptimo u octavo dato. ¿Cómo se podría resolver este problema? 🤔
Aquí es donde comenzamos a hablar de regresión lineal. Una regresión lineal es una aproximación numérica para modelar la relación entre una variable independiente X y una variable dependiente Y. Primero grafiquemos nuestros 5 datos [(1, 2), (2, 3), (3, 5), (4, 6), (5, 5)] para entender mejor lo que estamos tratando.
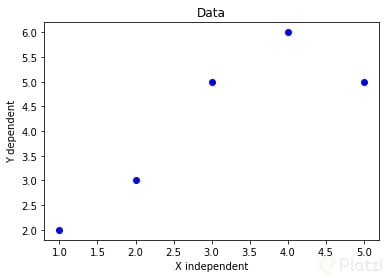
Una vez vistos los datos graficados queremos entender cuál es su comportamiento lineal. Como recordarás, la ecuación de una recta viene dada por y = b0 + b1x, donde b0 es la intersección con el eje y y b1 la pendiente. Por lo tanto, el objetivo es encontrar la ecuación de esa recta, es decir, tenemos que encontrar los coeficientes b0 y b1.
La técnica que usamos para obtener estos coeficientes se llama mínimos cuadrados. Este procedimiento consiste en minimizar la sumatoria del error entre el valor y real (medido) y el valor y de nuestro modelo de regresión.
Ajustando un línea recta por mínimos cuadrados
Como observarás, al error lo podemos representar con la siguiente ecuación:
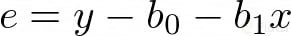
Teniendo en cuenta esto, procedemos a representar matemáticamente el método de mínimos cuadrados:
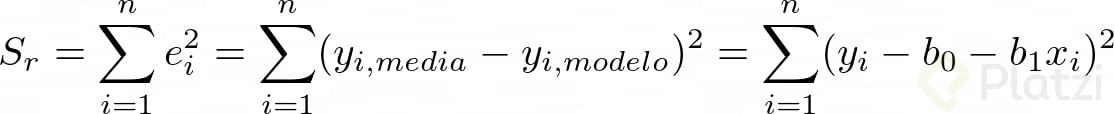
Para encontrar los valores de b0 y b1 derivamos la anterior expresión con respecto a cada una de estas variables:
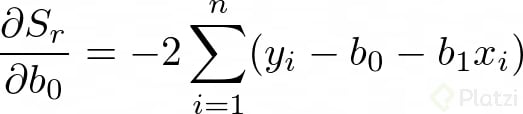
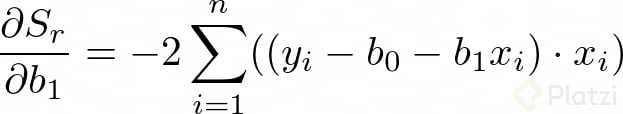
Dado que estamos buscando minimizar el error igualamos las derivadas a cero. Recuerda que en optimización igualamos a cero las derivadas para encontrar un máximo o un mínimo. Así tenemos:
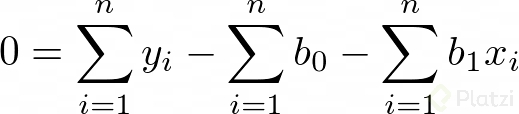
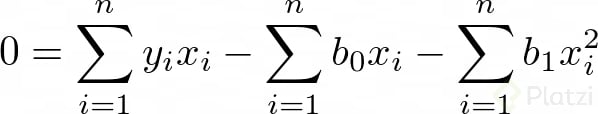
Luego, si consideramos que Σb0 = n*b0 (lo cual tiene sentido porque n es el número de datos), podemos expresar dos ecuaciones lineales de dos incógnitas:
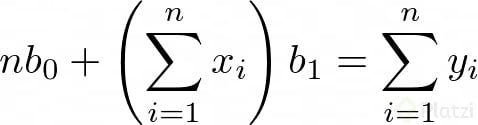
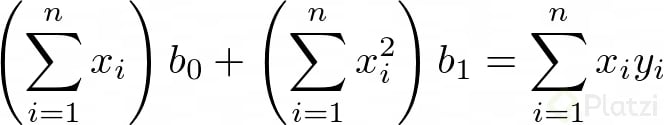
Ahora, si resolvemos para b0 y b1 obtenemos:
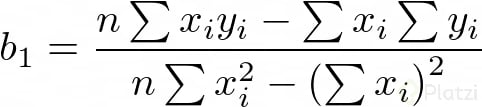
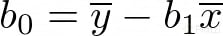
Donde ȳ y x̄ son las medias de x y y, respectivamente.
De esta forma hemos calculado los coeficientes b0 y b1 por el método de mínimos cuadrados. Si tenemos en cuenta los 5 datos sobre los que hablamos al inicio tenemos que b0 = 1.5 y b1 = 0.9. Esto nos da como resultado la curva de regresión que tenemos abajo:
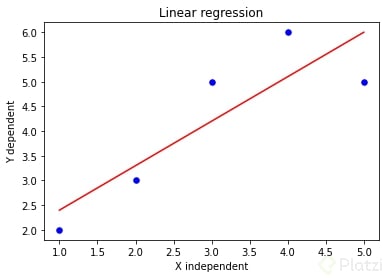
Y sí, a pesar de ser una línea recta, en matemáticas se le dice curva.
Ahora veremos la cuantificación del error, es decir, cuán erradas pueden ser nuestras predicciones.
¿Cómo puedo saber cuán reales son los datos modelados?
Consideremos que los datos siguen una distribución normal respecto a la línea de predicción y que el error es de magnitud similar a lo largo del data set. Esto se llama principio de máxima verosimilitud.
Para saber cuán erradas son nuestras predicciones debemos tomar en cuenta la suma total de los cuadrados de las diferencias entre los datos y la media St y la suma total de los cuadrados de las diferencias entre los datos y la curva de regresión Sr. Lo sé, esto parece un trabalenguas, pero miremos las fórmulas para que quede más claro:
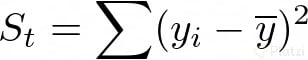
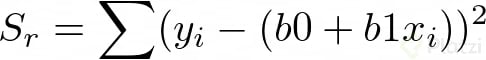
Ahora calculemos el error de aproximación entre estos dos valores, así:
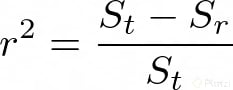
A r²se lo conoce como el coeficiente de determinación y a √(r²) como coeficiente de correlación. Entonces, cuando el coeficiente de correlación sea más cercano a 1 quiere decir que las predicciones serán menos erradas. En un caso ideal r será igual a 1, pero en tu carrera como Data Scientist casi nunca te encontrarás con un caso así. Es muy raro.
Una forma más práctica de representar el coeficiente de correlación, desde el punto de vista computacional, es:
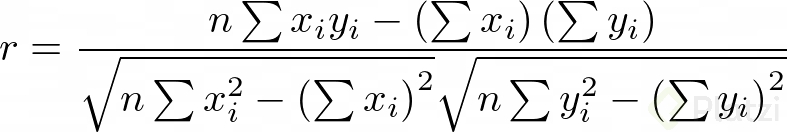
El coeficiente de correlación para nuestro ejemplo inicial es r = 0.867 lo cual está bien.
Ahora ya sabes de donde surge el modelo de regresión lineal y lo podrás aplicar en tus proyectos. Y claro, en tu carrera como Data Scientist lo harás a menudo. Me gustaría saber qué te ha parecido lo que acabas de aprender, cuéntamelo en los comentarios. También aprovecho para animarte a seguir con la Escuela de Data Science para que aprendas más sobre algoritmos. 💚
