La paradoja de Monty Hall demostrada con Python

El problema de Monty Hall es un problema de probabilidad inspirado en un viejo concurso de televisión llamado “Let 's Make a Deal”. El problema consiste en que un concursante tiene delante tres puertas, detrás de una de ellas hay un auto nuevo y en las otras dos hay cabras, el concursante debe adivinar en cuál puerta está el vehículo. Sin embargo, una vez el concursante elige una de las puertas, Monty Hall (El presentador que sabe que hay detrás de cada puerta) abre una de las puertas donde haya una cabra y le da la opción al concursante de cambiar de puerta que eligió. Por ello podríamos preguntarnos ¿Cambiar de puerta puede influir en el resultado del concurso? Al tener ahora dos puertas a elegir pensaríamos que tenemos 50% de probabilidad de acertar, sin embargo, esto no es así y resulta que tenemos un 66.66% de probabilidad de ganar si cambiamos la puerta que elegimos inicialmente. Esto lo podemos ver en el siguiente diagrama:

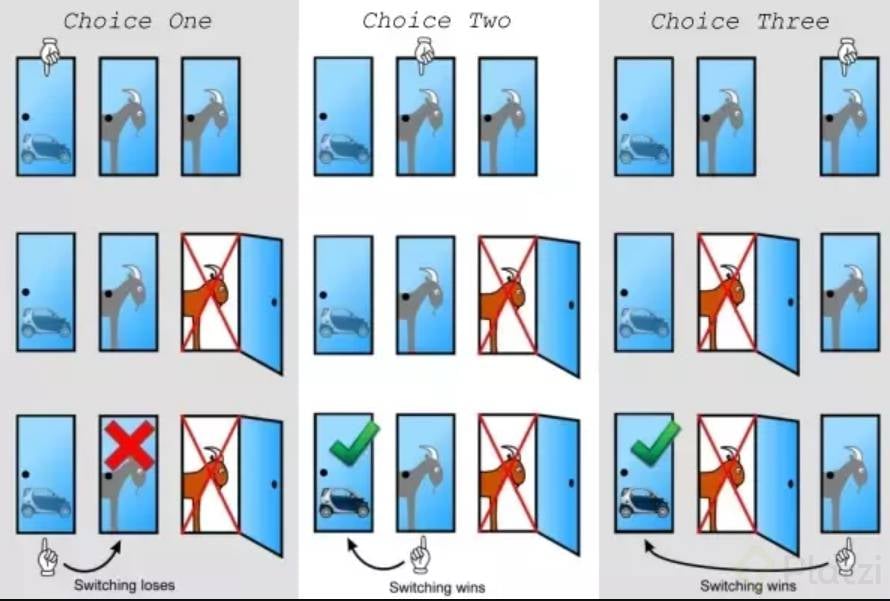
Si quieres tener más información del problema te dejo el siguiente link.

Simulemos esto en python:

# Monty Hall problem
import random

# Array with prizes of the doors
def random_door():
  doors = ["goat", "goat", "goat"]
  doors[random.randint(0, 2)] = "prize"
  return doors


# Monty Hall open a door
def open_door(player_sel, doors):
  open = player_sel
  if (doors[player_sel] == "prize"):
    open = random.randint(0, 2)
    while (open == player_sel):
      open = random.randint(0, 2)
    doors[open] = "open"
  else:
    index = doors.index("prize")
    while ((open == player_sel) or (open == index)):
      open = random.randint(0, 2)
    doors[open] = "open"

  return doors


def main():

  attemps = 1000000
  victories = 0
  defeats   = 0

  for i in range(attemps):
    # Generate the doors 
    doors = random_door()

    # Player selects the door
    player_selection = random.randint(0, 2)

    # Monty Hall opens a door with a goat
    doors = open_door(player_selection, doors)

    # Player changes of door
    if (player_selection == doors.index("prize")):
      player_selection = doors.index("goat")

    elif (player_selection == doors.index("goat")):
      player_selection = doors.index("prize")

    # Count of victories and defeats
    if doors[player_selection] == "prize":
      victories = victories + 1
    else:
      defeats = defeats + 1

  print(f"{attemps} attemps")
  print(f"You won {victories} times.")
  print(f"You lost {defeats} times.")

  print("Win percentage: {:.2f}%".format(((victories/attemps)*100)))


if __name__ == "__main__":
  main()

El código anterior es una simulación de la paradoja, por tanto empecemos a darle valores para verificar nuestra salida.

Resultado con 10 participaciones en el concurso:

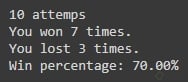
Resultado con 100 participaciones en el concurso:

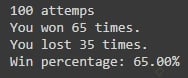
A primera vista parece que se aproxima un poco a 66,66%. Pero pongamos más cantidad de participaciones a ver cual es la tendencia.

Resultado con 1.000 participaciones:

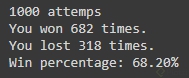
Resultado con 10.000 participaciones:

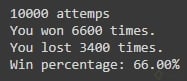
Resultado con 100.000 participaciones:

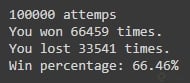
Fijémonos que cada vez que hacemos más intentos más se aproxima la probabilidad de ganar a 66.66%. Recuerda que cuando más nos acercamos al infinito este valor será cada vez más cercano a ⅔.

Resultado con 1.000.000 de participaciones:

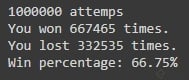
Nota: Al ser un algoritmo con varios valores random, como la elección del jugador, seguramente obtengas valores levemente diferentes.

Psdt: El script de Python se encuentra disponible en el siguiente repositorio:
https://github.com/CarlosDLA26/PythonScripts