Un punto (a,b) es llamado punto crítico o punto estacionario de f si:
(se utiliza fxx y fyy para referirse a las segundas derivadas parciales de x e y respectivamente, de igual manera fxy o fyx para las derivadas parciales mixtas.)
*fy -> derivada parcial de f respecto de y.
*fx -> derivada parcial de f respecto de x.
fy = 0 y fx = 0
Una función no necesariamente tiene valor máximo o mínimo en un punto crítico
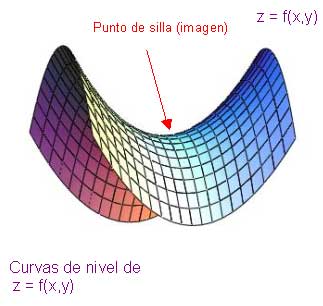
Por ejemplo en el punto (0,0) de un paraboloide se puede notar que ese punto es un máximo en dirección del eje x y un mínimo en dirección del eje y a este punto se llama punto silla.
Dados estos casos es necesario poder determinar si una funcion tiene o no un valor extremo en un punto crítico, para ese objetivo se aplica la prueba de la segunda derivada.
Se supone que el punto (a,b) es un punto crítico de f, entonces podemos hallar D
D = D(a,b) = fxx(a,b)*fyy(a,b)-[(fxy(a,b)^2)]
CASO 1: D > 0 y fxx(a,b) > 0 entonces f(a,b) es un mínimo local.
CASO 2: D > 0 y fxx(a,b) < 0 entonces f(a,b) es un máximo local.
CASO 3: D < 0, entonces f(a,b) no es un mínimo ni un máximo y se puede considerar como punto silla.
(En caso de que D = 0 no se puede concluir nada sobre ese punto).
-Fuentes bibliográficas: Calculo de varias variables trascendentes tempranas septima edición James Stewart.
Curso de Cálculo Multivariable
