Teoria de conjuntos

Teoria de conjuntos:
Podemos entenderla como la herramienta que nos pertmite utilizar los conjuntos para analizar, clasificar y ordenar conocimientos y generar una red conceptual de almacenamiento.

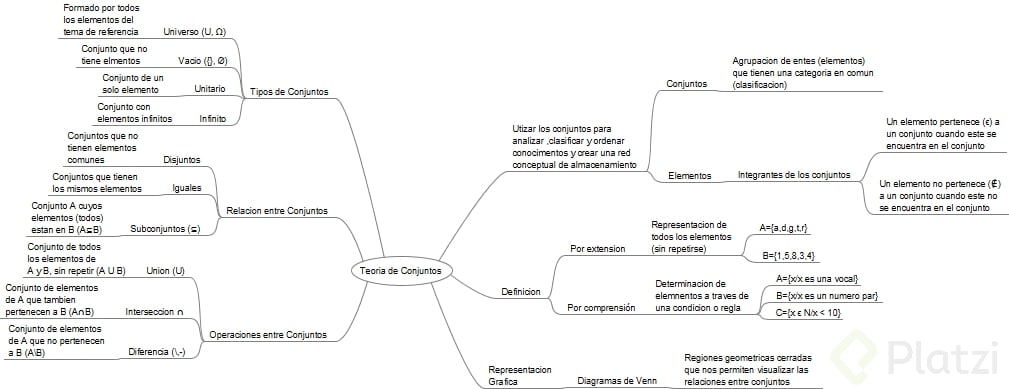
Conceptos básicos
Conjunto: Agrupacion de entes (elementos) con una caracteristica en común (clasifacion)
Elemento: Unidad basica del conjunto, es decir cada integrante del conjunto.

Definicion de Conjuntos:

• Extension: Cuando se mencionan todos los elementos sin repetirse.
  Ejemplos:
  A={1,3,9,5}
  B={t, r, s, f, h, l}
• Compresion: Los elementos se determinan a traves de una condición o regla
  Ejemplos:
  A={x/x es un numero natural menor a diez}
  B={x/x es una vocal}

Representacion Grafica:
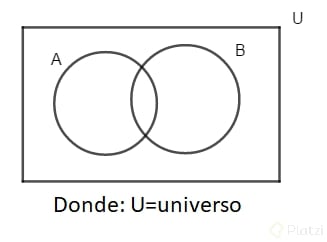
Diagramas de Venn: regiones geometricas (cerradas) que nos permiten visualizar las relaciones entre los conjuntos

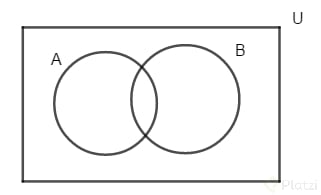
Tipos de Conjuntos:

• Universo (U, Ω) Formado por todos los elementos del tema de referencia

• Vacio ({ }, Ø) Conjunto sin ningun elemento
  Ejemplos:
  A={rinocerontes nacidos de un huevo}
  B={numeros menores a 1 y mayores a 2}
  C={}
  

• Unitario: conjunto con solo un elemento
  A={1}
  B={c}
  C={vocales de la palabra paz}

• Infinito: conjunto con una cantidad infinita de elemntos
  A={x/x es un numero natural}
  B={x/x es un numero real entre 1 y 2}
  C={}

Relaciones entre conjuntos:

• Disjuntos: Conjuntos que no tienen elementos en comun
• Iguales: Conjuntos que tienen los mismos elementos
• Subconjunto: (⊆) Conjunto A cuyos elementos (todos) están en B (A⊆B)

Operaciones con conjuntos:
-Union(U): AUB: conjunto de todos los elementos de A y B (sin repetir)

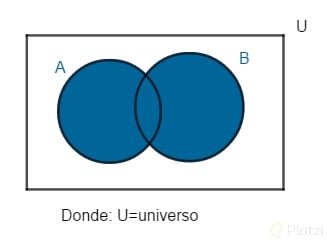
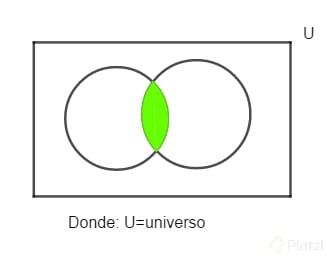
-Interseccion(∩): A∩B: conjunto de todos los elementos que pertenecen tanto a A como a B

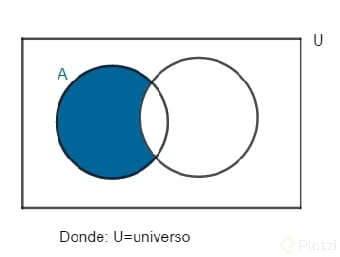
-Diferencia (/,-): A/B: conjunto de elementos que pertenecen a A y no pertenecen a B