En esta oportunidad haremos que nuestra maquina aprenda a realizar operaciones a traves de una Regresion Lineal, por motivos de eficiencia solo usaremos la libreria Numpy
1-Definimos una clase que sera nuestra Regresion Lineal, definimos nuestro learning rate(lr), el numero de iteraciones, nuestro training dataset(x para nuestros features y y para nuestros labels), y nuestros pesos que seran inicializados en 0.Espero que se haya entendido.
La forma de nuestra regresion lineal es esta:
y = wx+b
Solo que en esta oportunidad no usaremos bias ya que no es un problema muy complejo, por lo que nuestro modelo tendra esta forma:
y = wx
classLinear_regression:def__init__(self, x, y, lr = 0.01, iteraciones = 2000):
self.lr = lr
self.iteraciones = iteraciones
self.x = x
self.y = y
self.pesos = np.zeros((x.shape[1], 1))
2-Definimos nuestro metodo de entrenamiento, traves de cada iteracion lo que hacemos es:
Obtener nuestra prediccion, igual a wx
El gradiente, que es la derivada parcial de nuestra funcion de coste y se reduce a esto: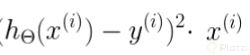
Donde h(x) son nuestras predicciones, y nuestros labels, x nuestros features.
Actualizar nuestros pesos, con esta formula: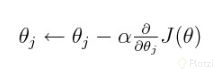
Donde J(o) es nuestra funcion de coste y alfa nuestro learning rate, pero como ya sabemos cual es la derivada parcial de J(o) tendremos esto: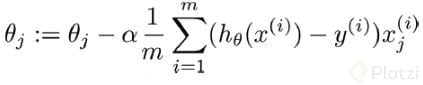
deftraining(self):
perdidas = []
n = y.shape[0]
for i in range(self.iteraciones):
prediccion = x.dot(self.pesos)
residual = prediccion - y
gradiente = x.T.dot(residual)
self.pesos -= (self.lr * gradiente)/n
costo = np.sum(residual**2)/n
perdidas.append(costo)
3-Calculamos el costo con la formula del MSE:

Y guardamos cada costo en una lista llamada perdidas, finalmente retornamos esa lista
4-Finalmente creamos nuestro metodo de entrenamiento, multiplicando nuestros inputs por nuestros pesos.
defpredecir(self, inputs):return np.dot(inputs,self.pesos)
Ahora pondremos a prueba nuestro modelo, y vamos a plotear nuestras perdidas con el paso de las iteraciones con la ayuda de matplotlib, la forma de la ecuacion que le enseñaremos sera: y = x1 + x2 - x3
import matplotlib.pyplot as plt
import numpy as np
classLinear_regression:def__init__(self, x, y, lr = 0.01, iteraciones = 2000):
self.lr = lr
self.iteraciones = iteraciones
self.x = x
self.y = y
self.pesos = np.zeros((x.shape[1], 1))
deftraining(self):
perdidas = []
n = y.shape[0]
for i in range(self.iteraciones):
prediccion = x.dot(self.pesos)
residual = prediccion - y
gradiente = x.T.dot(residual)
self.pesos -= (self.lr * gradiente)/n
costo = np.sum(residual**2)/n
perdidas.append(costo)
return perdidas
defpredecir(self, inputs):return np.dot(inputs,self.pesos)
x = np.array([[4,4,5],[2,3,1],[4,6,5],[10,6,7],[9,4,4],[9,3,8]])
y = np.array([[3],[4],[5],[9],[9],[4]])
#y = x1 + x2 - x3
modelo = Linear_regression(x = x, y = y)
losses = modelo.training()
print(modelo.predecir([2,5,3]))
plt.plot(losses)
Output:

Nuestra perdida es 0, nuestro modelo predijo con exactitud la ecuacion y por ende podemos decir que nuestro modelo tiene un accuracy de un 100%, es decir.aprendio muy bien.
Podemos usar este modelo para cosas mas complejas, pero tendremos que hacer unas configuraciones extra, como cambiar nuestro learning rate(0<lr<1), el numero de iteraciones o darle mas datos a nuestro modelo.
