Nivel de confianza y valor de Z

Hemos visto en ejemplos que cuando dicen que hay un 95% el coeficiente o el numero de sigmas (desviaciones estándar) es 1.96, pero, ¿De donde sale ese número?, En este tutorial pretendo explicar cómo podemos hallar ese valor o el valor para distintos niveles de confianza.

De entrada quiero que tengan en mente de que la curva normal tiene dos lados que son totalmente simétricos.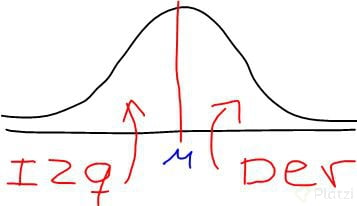

Sabemos que la suma de todas las probabilidades en un evento debe ser 1, entonces, supongamos que el área debajo la curva normal representa el total de probabilidades, osea 1, pero podemos decir que el área total debajo de la curva normal es la suma de la probabilidad del lado izquierdo + la probabilidad del lado derecho que seria P(izq) + P(der) = 0.5 + 0.5, dado que, como la curva es simétrica pues podemos decir la probabilidad de cada lado es 0.5.

¿Qué tiene que ver eso con el 1.96 cuando la confianza es del 95%?
Bueno, si nos piden una confianza del 95%, podemos decir que debemos llenar el área de la curva pues en un 95%, entonces, si 1 es el área total de la curva normal, podemos decir que el 95% del área es 0.95 verdad?, entonces, eso quiere decir que nos falta 1-0.95 = 0.05 para llenar el área de la curva normal, peeero , nosotros sabemos que la curva tiene dos partes (izquierda y derecha), entonces para saber cuanto le falta a cada lado lo único que debemos hacer es dividir lo que falta para llenar el área (osea 0.05) entre 2 y de esa manera obtenemos 0.025.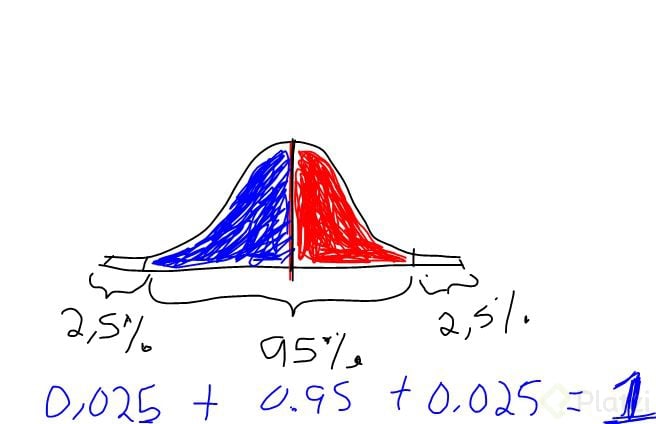

sabiendo que a cada lado le falta 0.025 pues con ese valor ahora nosotros podemos usar una tabla de valores de Z (Z viene siendo el coeficiente de sigma) para saber a qué valor le pertenece el 0.025.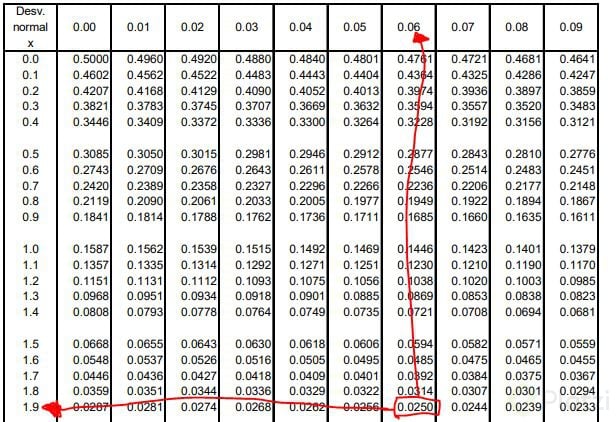

como podemos ver, lo único que debemos hacer es buscar el 0.025 entre todos los valores de la tabla y ver si “ubicación”. En este caso la ubicación de 0.025 está en 1.9 y 0.06, entonces lo único que debemos hacer ahora es sumar esos valores y así obtenemos el 1.96.
conociendo ese valor, ahora también podemos sacar los intervalos de confianza (Los intervalos de confianza nos dicen entre qué valores se encuentran la mayoría de nuestros datos)
el intervalo para un 95% de confianza sería entre (µ- 1.96σ) y (µ+ 1.96σ), donde µ es la media de tus datos y σ la desviación estándar de tus datos.

EJEMPLO PARA QUE QUEDE MÁS CLARO
Si ustedes quieren una confianza del 99% pues primero deben calcular cuanto falta en cada lado de la curva, en este caso seria (1 - 0.99) / 2 = 0.005.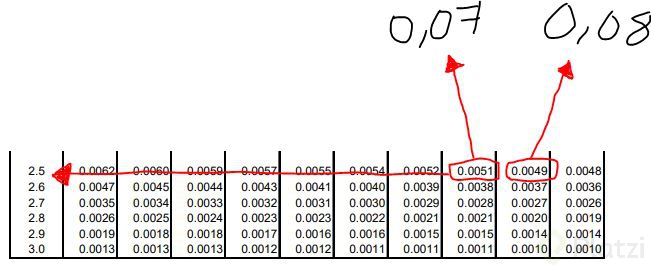

si buscamos el 0.005 en la tabla nos daremos cuenta de que no está, pero hay 2 valores cercanos a el que son 0.0051 y 0.0049, entonces si nosotros hallamos le media pues nos dá (0.0051 + 0.0049) / 2 = 0.005. Entonces eso mismo debemos hacer con sus respectivos valores de Z para hallar el valor de Z para 0.005.
El Z de 0.0051 seria 2.57 y el Z de 0.0049 seria 2.58, entonces la media de esos valores es (2.57 + 2.58) / 2 = 2.575. Conociendo ese valor, ahora podemos decir que el Z (coeficiente de sigma) para un 99% de confianza es 2.575

Entonces el intervalo de confianza estaría entre (µ- 2.575σ) y (µ+ 2.575σ).
link de la tabla: http://halweb.uc3m.es/esp/Personal/personas/amalonso/esp/Tablas.pdf (Es la primera tabla que dice distribución normal).
Eso es todo, espero haber clarificado alguna de sus posibles dudas.

Pd: Si desean tutorial de algún otro tema relacionado con estadística, cálculo(diferencial o integral) y algebra lineal pueden ponerlo en comentarios. gracias