Trabajaremos nuestro ejemplo agrupando los datos de la siguiente tabla
| Punto | x | y |
|---|---|---|
| A1 | 2 | 10 |
| A2 | 2 | 5 |
| A3 | 8 | 4 |
| A4 | 2 | 7 |
| A5 | 7 | 5 |
| A6 | 6 | 4 |
| A7 | 1 | 2 |
| A8 | 4 | 9 |
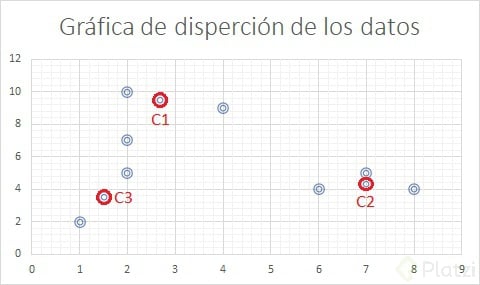
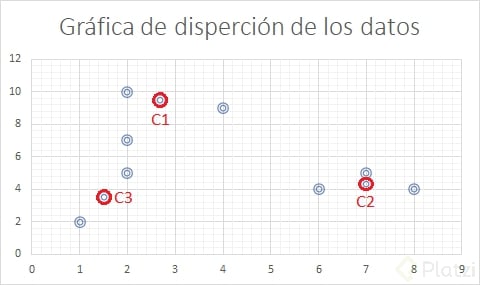
La gráfica de dispersión de datos inicial es la siguiente, donde podemos identificar los puntos de referencia en torno a los cuales trabajaremos.
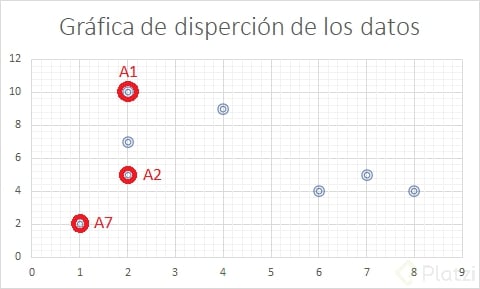
Iteración 1.
Los centroides identificados son:
-
C_1 = (2,10) = A1
-
C_2 = (2,5) = A2
-
C_3 = (1,2) = A7
El análisis de distancias para el centroide A1:
Para realizar el análisis de las distancias euclidianas se utilizará la siguiente ecuación en cada uno de los casos:
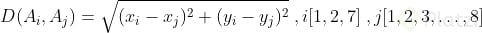
De esa forma se genera la siguiente tabla de datos:
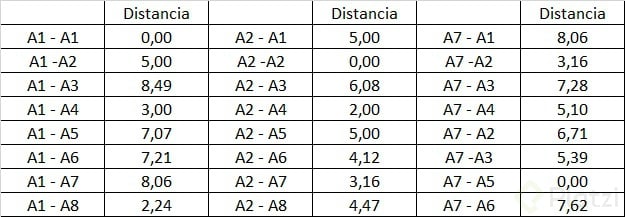
Obtenemos entonces la matriz de distancias euclidianas para nuestra primera iteración:

Identificando el menor valor de cada columna en la matriz anterior y asignándole un uno formaremos la siguiente matriz de agrupamiento.

Con estos datos procederemos a calcular las posiciones de los nuevos centroides:
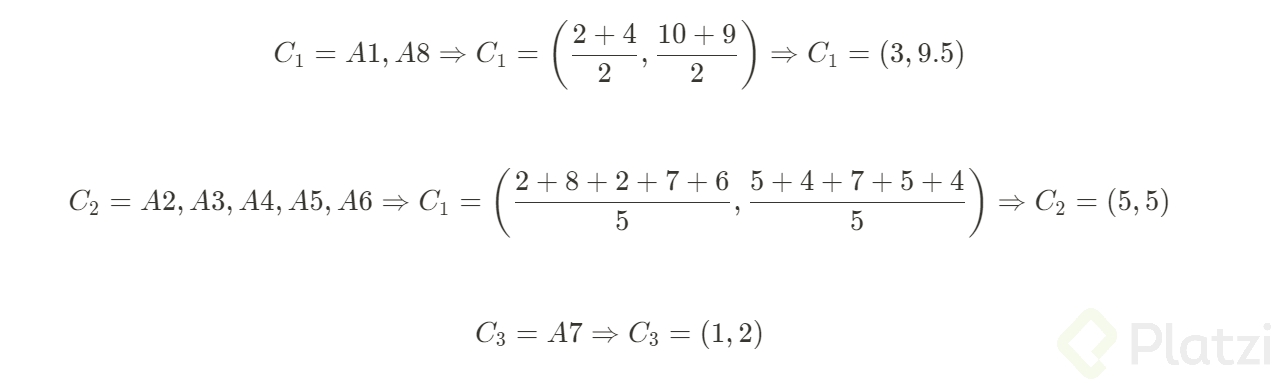
Como podemos observar los últimos clusteres obtenidos se han mantenido constantes con respecto a la iteración anterior, de igual forma podemos ver que ocurre lo mismo en la última gráfica de dispersión por lo tanto podemos concluir que se han estabilizado.
Iteración 2.
Generamos la siguiente tabla de datos:
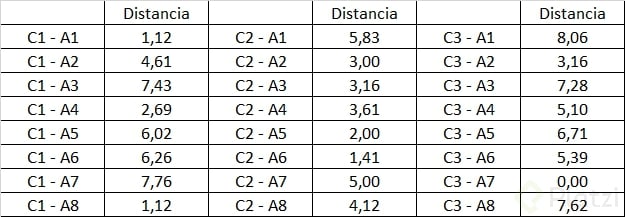
Obtenemos entonces la matriz de distancias euclidianas para nuestra primera iteración:

Identificando el menor valor de cada columna en la matriz anterior y asignándole un uno formaremos la siguiente matriz de agrupamiento.

Con estos datos procederemos a calcular las posiciones de los nuevos centroides:
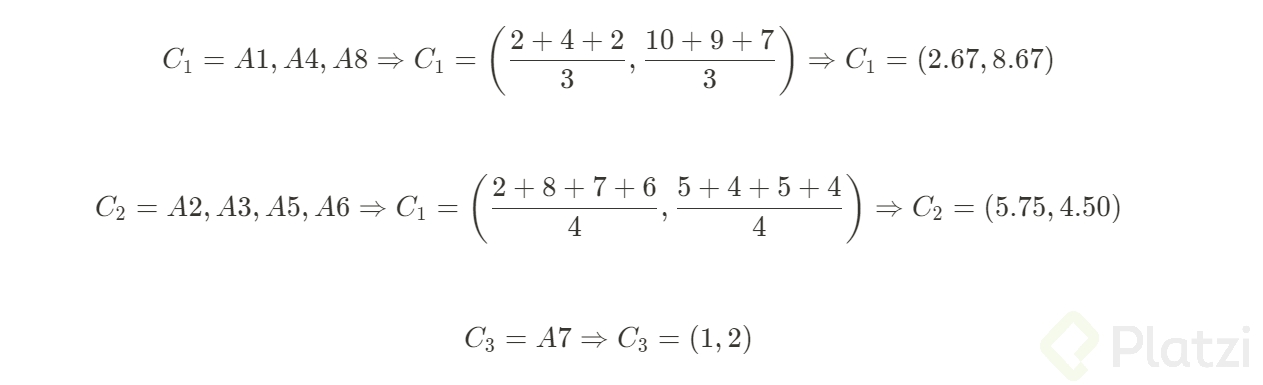
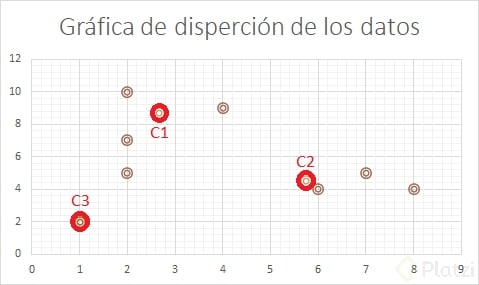
Como tenemos un nuevo cluster tendremos que volver a analizar en una siguiente iteración.
<h1>Iteración 3.</h1>Generamos la siguiente tabla de datos:
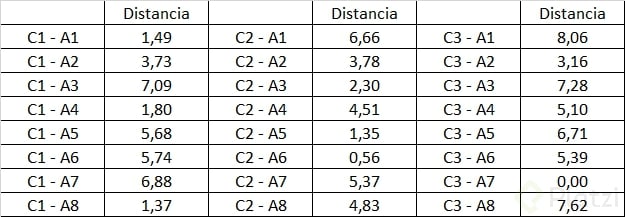
Obtenemos entonces la matriz de distancias euclidianas para nuestra tercera iteración:

Identificando el menor valor de cada columna en la matriz anterior y asignándole un uno formaremos la siguiente matriz de agrupamiento.

Con estos datos procederemos a calcular las posiciones de los nuevos centroides:
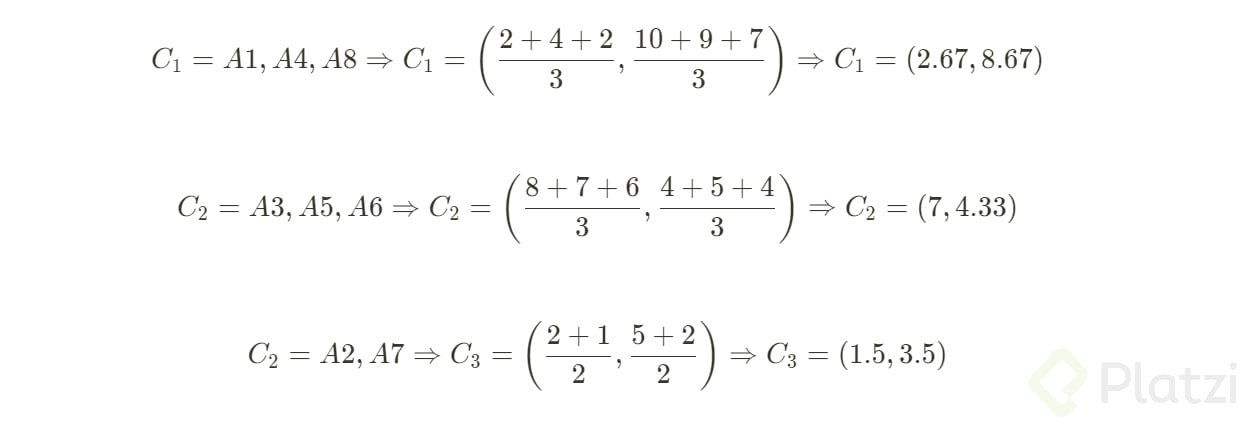
Como tenemos un nuevo cluster tendremos que volver a analizar en una siguiente iteración.
Iteración 4.
Generamos la siguiente tabla de datos:
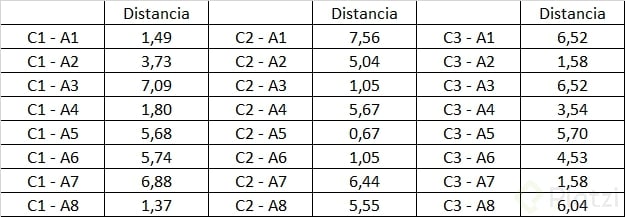
Obtenemos entonces la matriz de distancias euclidianas para nuestra primera iteración:

Identificando el menor valor de cada columna en la matriz anterior y asignándole un uno formaremos la siguiente matriz de agrupamiento.

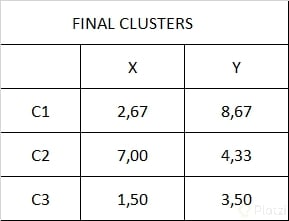
Con estos datos procederemos a calcular las posiciones de los nuevos centroides:
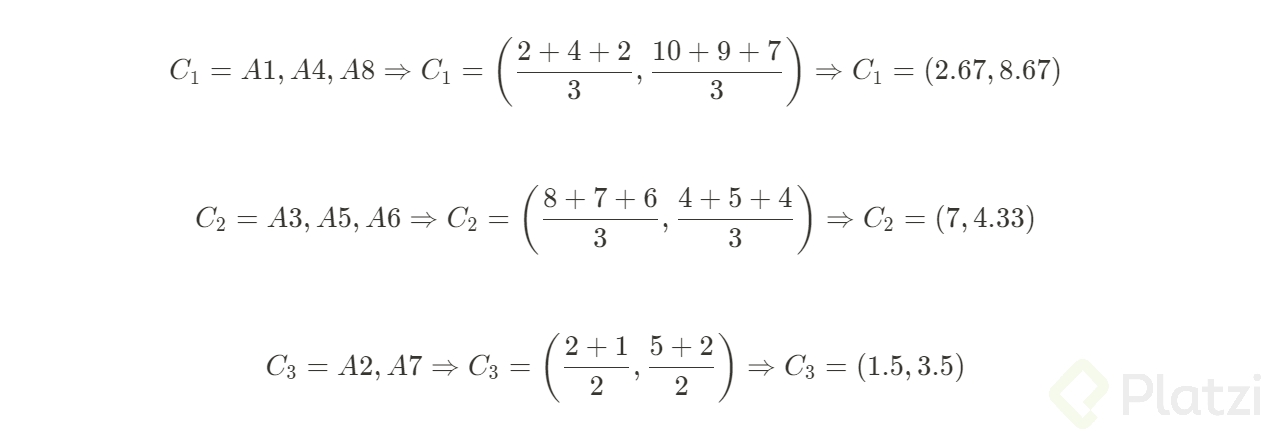
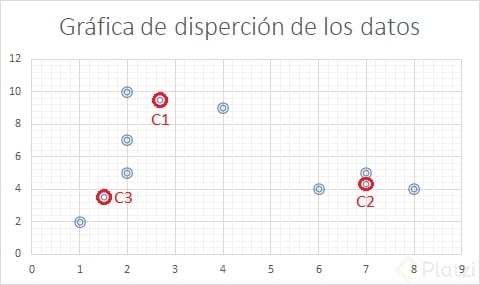
Como podemos observar los últimos clusteres obtenidos se han mantenido constantes con respecto a la iteración anterior, de igual forma podemos ver que ocurre lo mismo en la última gráfica de dispersión por lo tanto podemos concluir que se han estabilizado.
Curso de Introducción al Pensamiento Probabilístico
COMPARTE ESTE ARTÍCULO Y MUESTRA LO QUE APRENDISTE




