Método Elbow, para elegir el número ideal de clusters

Método Elbow

El método Elbow o **codo ** nos ayuda a elegir el número optimo de clústers, cuando buscamos hacer clasificación en un conjunto de datos. Para hacer uso de este método partimos del cálculo de la distorsión promedio de cada clúster, esto es la distancia de cada elemento con su centroide correspondiente.

Para el calcular la distorsión usamos:

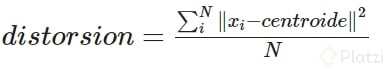
donde:
N es el numero de elementos

Esta información la encontramos en clustering_objetive, que nos retorna justamente la distorsión.

defclustering_objective(data, grouping, centroids):
    J_obj = 0for i in range(len(data)):
        for j in range(len(centroids)):
            if grouping[i] == (j+1):
                J_obj += np.linalg.norm(data[i] - centroids[j])**2
    J_obj = J_obj/len(data)
    return J_obj    

Aplicando el método

Para encontrar el número optimo de clústers, se calcula el modelo de clasificación variando el número de clusters

defelbow(data, n_clusters):
    distortion = []
    for i in range(n_clusters):
        model = Kmeans_alg(data, data[:i+1])
        distortion.append(model[2][-1])

    return distortion

Al asignar y evaluar la función tenemos una lista con la distorsión de cada clúster, para este ejemplo probamos con 7 clústers.

x = elbow(X, 7)

# Resultado[1.0445545995284504,
 0.4615489151214897,
 0.1562876164551304,
 0.1363687839406393,
 0.12400494851224586,
 0.10497968520514046,
 0.08792892682033376]

Cuando se grafican estos valores contra el número de clúster:

Buscamos la parte de la gráfica donde la línea es menos suave o cambia abruptamente lo que forma un “codo”, ese número de clúster ayudará al momento de clasificar los datos.

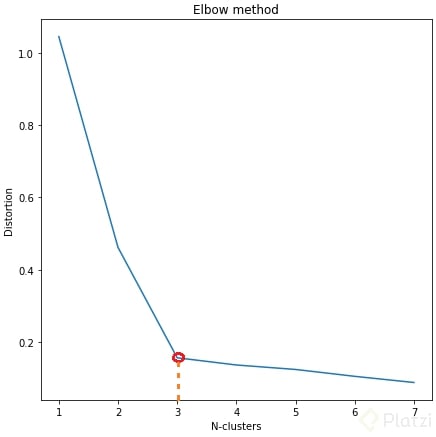
Se puede notar la diferencia en la clasificación, graficando cada caso.

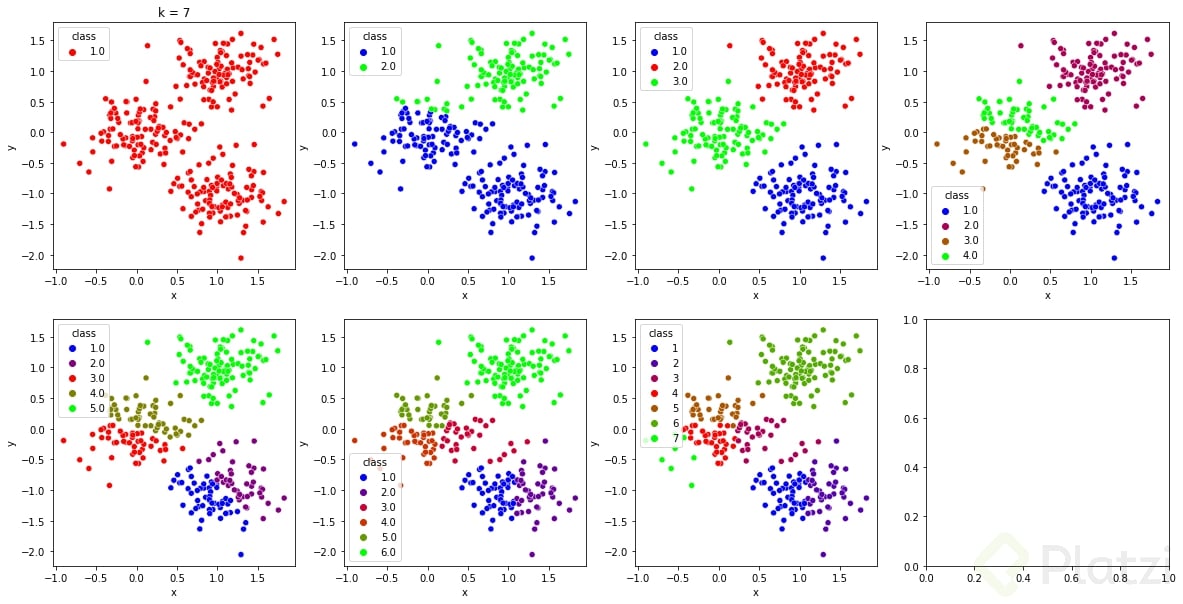
Nota: Los datos del ejemplo son de la clase 27 del curso.