Funciones de activación de una neurona - 👩‍💻🧑‍💻

El día de hoy estaré compartiendo con ustedes mis apuntes de clase, específicamente, los de funciones de activación.

Una definición muy básica y sencilla de una función de activación es que se encargan de devolver una salida a partir de un valor de entrada, o en otras palabras, se usan para propagar la salida de los nodos de una capa hacia la siguiente capa.

• Función de paso escalonado (escalón binario):

Son funciones que tienen diferentes valores definidos por un intervalo. Por ejemplo la función escalón de Heaviside:

Ya hemos visto un ejemplo de ella, en la clase de funciones algebraicas.

• Función Sigmoide:

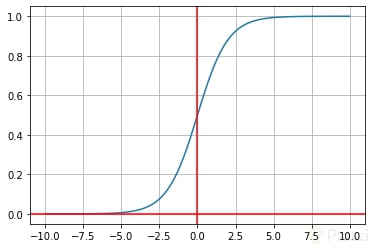
La función sigmoide transforma los valores introducidos a una escala (0,1), donde los valores altos tienen de manera asintótica a 1 y los valores muy bajos tienden de manera asintótica a 0.

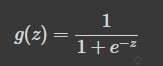
Y con este sencillo código pueden encontrar una representación de tal función de activación:

import numpy as npimport matplotlib.pyplot as pltimport math

N = 100

x = np.linspace(-10,10,num=N)

z= 1/(1 + np.exp(-x))

fig, ax = plt.subplots()
ax.plot(x,z)
ax.axhline(y=0, color='red')
ax.axvline(x=0, color='red')
plt.grid()

• Función tangente hiperbólica:

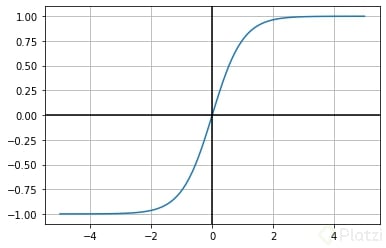
La tanh representa la relación del seno hiperbólico al coseno hiperbólico: tannhx=sinhx/cosh . A diferencia de la Función Sigmoidea, el rango normalizado de tanh es de [−1,1] . La ventaja de tanh es que puede manejar más fácilmente los números negativos.

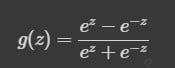
Nuevamente, ilustramos dicha función de activación con un sencillo código con el fin de facilitar la visualización y el entendimiento.

import numpy as np
import matplotlib.pyplot as plt
import math

N = 100
x = np.linspace(-5,5,num=N)
z= (np.exp(x) - np.exp(-x))/(np.exp(x) + np.exp(-x))

fig, ax = plt.subplots()
ax.plot(x,z)
ax.axhline(y=0, color='black')
ax.axvline(x=0, color='black')
plt.grid()

• Función ReLU o Rectificación lineal:

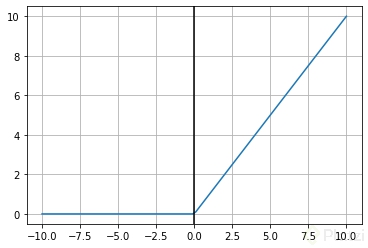
Las funciones de Rectificado lineal son transformaciones que activan un nodo sólo si la entrada está por encima de una cierta cantidad. Mientras la entrada es inferior a cero, la salida es cero, pero cuando la entrada supera un cierto umbral, tiene una relación lineal con el dependiente variable:

con una imagen:

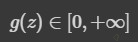
Y aquí un sencillo código para ilustrar dicha función de activación:

import numpy as np
import matplotlib.pyplot as plt

deff(x):
  y = np.zeros(len(x))
  for idx,x in enumerate(x):
    ifx >= 0:
      y[idx] = xreturn y

x = np.linspace(-10, 10, num=100)

y= f(x)

fig, ax = plt.subplots()

ax.plot(x,y)
# ax.axhline(y=0, color='black')
ax.axvline(x=0, color='black')

ax.grid()

Estos son mis apuntes de la clase Funciones de activación de una neurona, en la que he logrado ejemplificar por medio de sencillos códigos cómo los visto en clase, con el uso de las mismas librerías cómo Numpy y Pyplot, las funciones presentadas. En mi caso, conocía un poco estas funciones por mis clases de Control de Procesos en la Universidad, sin embargo, recordarlas e implementarlas en Python me han ayudado mucho.
Te invito a que si encuentras algún error, o una forma más sencilla de explicar algo de lo expuesto aquí, lo dejes en los comentarios y me lo hagas saber, espero les sirva de algo a todos. Muchos éxitos…

Si quieren ver el Notebook completo, pueden verlo en: ¿Cómo se compone una neurona?