vaya que le he dedicado tiempo a entender esto de la regresión lineal y el descenso del gradiente. Quiero dejarles todo este aprendizaje plasmado en un ejercicio que vamos a resolver tanto por regresión lineal como por descenso del gradiente. El ejercicio está basado en unas clases del canal DotSCV, pero aquí trato de incluir cositas adicionales para complementar dicho tutorial, el cual les dejo a continuación para que lo revisen.
https://www.youtube.com/playlist?list=PL-Ogd76BhmcCO4VeOlIH93BMT5A_kKAXp
Lo primero son los datos con los que vamos a trabajar (el dataset), el cual corresponde a el precio de las viviendas en Boston en función del número de habitaciones.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
boston = load_boston()
X = boston.data[:,5]Y = boston.target
La variable “X” contiene el número de habitaciones de cada vivienda del dataset. La variable Y contiene el precio de las viviendas.
Del curso de regresión lineal (el cual supongo que ya hiciste si vienes realizando la carrera de Data Science) aprendimos que la ecuación de una recta es de la forma:
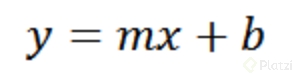
donde m es la pendiente de la recta y b es el punto de corte con el eje y
También aprendimos que podemos hallar la m aplicando regresión lineal con la siguiente fórmula:
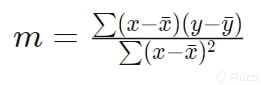
teniendo hallada la pendiente y sabiendo que la línea de regresión debe pasar por los promedios de X y Y, se reemplazan estos datos en la ecuación de la recta y así obtenemos b
defregresion():
mean_x, mean_y = np.mean(X), np.mean(Y)
numerador = np.sum((X-mean_x)*(Y-mean_y))
denominador = np.sum(X*(X-mean_x))
m = numerador / denominador
b = mean_y - m*mean_x
return (m, b)
defgraficar():
plt.scatter(X,Y, alpha=0.3)
y_pred = m*X + b
plt.plot(x, y_pred, color = "b")
m, b = regresion()
print("m = {}, b ={}".format(m, b))
graficar()
otra forma de realizar la regresión es por medio de matrices como se explica en este video: https://www.youtube.com/watch?v=k964_uNn3l0&ab_channel=DotCSV y cuyo código es el siguiente (explicación detallada en los enlaces que he dejado):
X_raw = boston.data[:,5]
Y = boston.target
# columna de 1s para termino independiente
X = np.array([np.ones(len(X_raw)), X_raw]).T
B = np.linalg.inv(X.T @ X) @ X.T @ Y
print("b = {}, m={}".format(B[0], B[1]))
obteniendo así el mismo resultado por cualquiera de las dos regresiones realizadas. El resultado fué el siguiente:
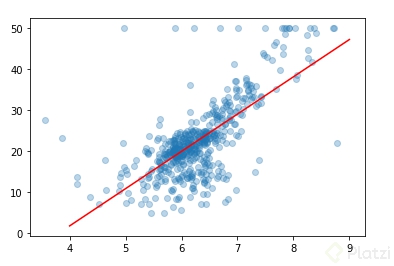
AHORA EL DESCENSO DEL GRADIENTE!!!
Aplicando el descenso del gradiente a este mismo dataset. Para ello necesitamos una función de coste como la vista en el curso.
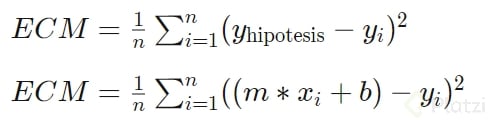
donde la y_hipotesis corresponde a la predicción realizada a partir de valores de m y b aleatorios.
Para este caso, la función de coste es la sumatoria de todos los puntos del dataset, por lo que el gradiente no lo podemos calcular como se vio en el curso (en el que usábamos un h para hallarlo)
sino que es necesario obtener las derivadas parciales de la función:
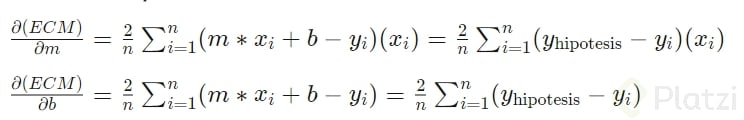
Que no te asusten las anteriores ecuaciones, podrías calcularlas aplicando regla de la cadena. Como los parámetros que estamos optimizando son m y b pues derivamos respecto a ellos y así obtenemos las derivadas parciales.
Ahora sí, el codigo:
# en "theta" se guarda [m, b]# los inicio con valores cualquiera
theta = np.array([0,0])
lr = 0.01
grad = np.zeros(2)
tamano = len(X)
defcoste(m, b):
error = 0for i in range(tamano):
hipotesis = m*X[i]+b
error += (hipotesis - Y[i])**2return error/tamano
defgradiente(m, b):
m_sum = 0
b_sum = 0for i in range(tamano):
hipotesis = m*X[i] + b
m_sum += (hipotesis - Y[i]) * X[i]
b_sum += (hipotesis - Y[i])
grad[0] = 2*m_sum/tamano
grad[1] = 2*b_sum/tamano
return grad
fig, axs = plt.subplots(2,1)
axs[0].scatter(X,Y, alpha=0.3)
for i in range(10000):
theta = theta - lr * gradiente(theta[0], theta[1])
error = coste(theta[0], theta[1])
axs[1].plot(i, error, "o")
y_pred = theta[0]*X + theta[1]
axs[0].plot(X, y_pred, c="red")
print("m = {}, b ={}".format(theta[0], theta[1]))
Cosas importantes
El resultado es el siguiente:
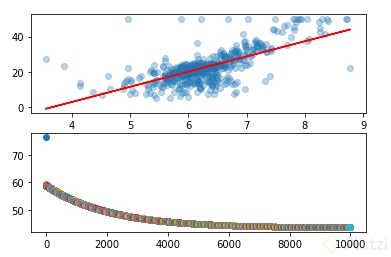
Quedo atento a cualquier duda, corrección o sugerencia.
