Para este experimento tome de kaggle el dataset de California Housing Prices
El objetivo es predecir el valor medio de los inmuebles,
Iré al grano mostrando el proceso de escalamiento y los resultados, dejo acá el colab con el procedimiento completo.
Antes de escalar los datos dividiré en train y test y los escalare por separado, como comenta Carlos Alarcon en el curso de Curso de Fundamentos de Redes Neuronales con Python y Keras, los datos de test no deben poseer información de los datos de train, ya que incurrimos en faltas éticas y aparte conlleva a que nuestro modelo presente overfitting.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(features_fill, target, test_size=0.2)
Para el escalamiento usé la función tanh(x/a)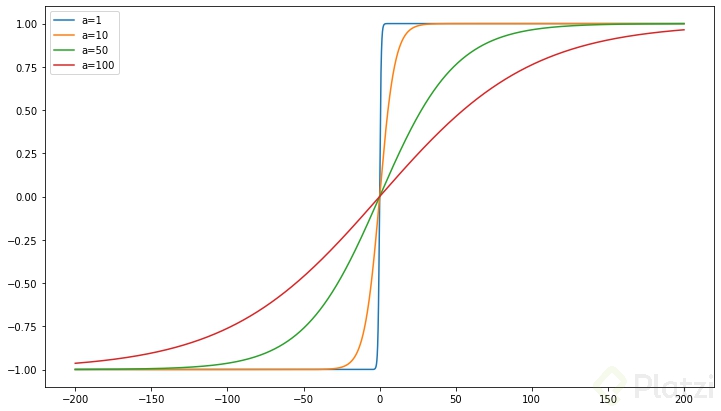
Donde:

Los métodos de escalamiento con los que haré las comparaciones son:
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
from sklearn.preprocessing import RobustScalerTambién durante el proyecto decidí buscar con varios métodos de regresión, y ver cual me daba los mejores resultados.
Estos son los que use:
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_errorObservemos los resultados al evaluar: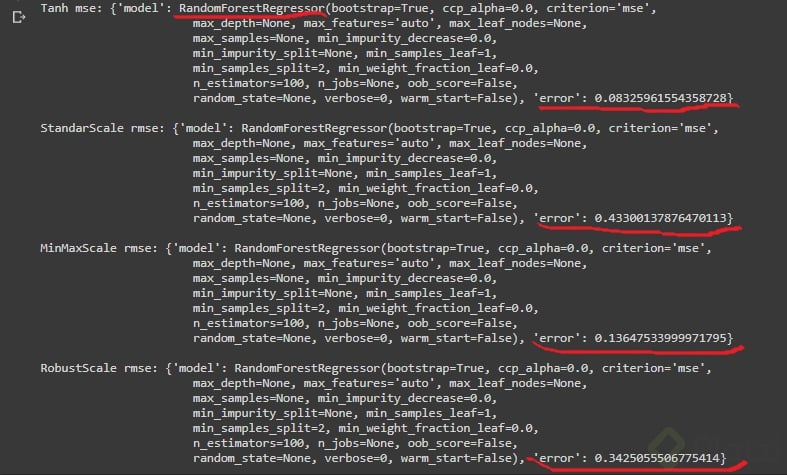
Obtenemos valores muy pequeños que a simple vista no representan valores de casas, entonces procedemos a re-escalar estos resultados. Para esto las funciones de Scikitlearn cuentan con el método inverse_transform. Solo lo aplicamos a nuestro resultado y obtenemos: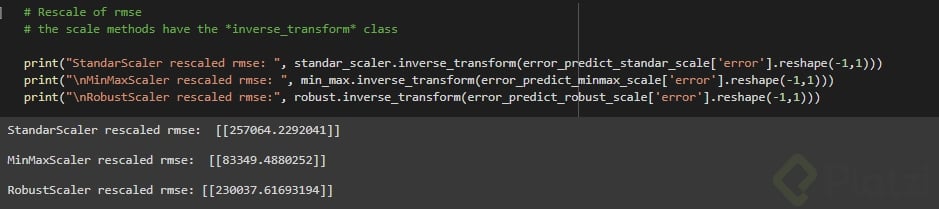
Cuando re-escalamos el resultado de la escala tanh
usando la fórmula


Esta super amigo, voy a usarlo, te cuento me gusta mas Deepnot
Hola! tengo una duda.
Tenía entendido que deberías escalar los datos en el set de test con las mismas medias (promedios) del set de entrenamiento? Cuál es la diferencia de hacerlo así?
Hola! tienes razón en su momento lo hice así por un comentario de otra clase:
"los datos de test no deben poseer información de los datos de train, ya que incurrimos en faltas éticas y aparte conlleva a que nuestro modelo presente overfitting."Pero investigando un poco encontré esto:
No se deben recalcular los parámetros de escalamiento (como el mínimo y el máximo para la normalización o la media y la desviación estándar para la estandarización) en función de los datos de prueba por varias razones:
1.- Consistencia: El propósito principal del escalamiento es garantizar que las características tengan la misma escala en los datos de entrenamiento y los datos de prueba. Si recalculas los parámetros de escalamiento en los datos de prueba, podrías obtener una escala diferente, lo que rompería la consistencia entre los dos conjuntos de datos.
2.- Evitar fugas de información: Recalcular los parámetros de escalamiento en los datos de prueba podría introducir una forma de fuga de información. Esto significa que estarías utilizando información de los datos de prueba para ajustar la transformación, lo cual no es apropiado, ya que los datos de prueba deberían tratarse como datos completamente nuevos que el modelo nunca ha visto antes. Esto podría llevar a una evaluación sesgada y poco realista del rendimiento del modelo.
3.- Mantener la misma escala de entrenamiento: La escala de las características en el conjunto de datos de entrenamiento se selecciona generalmente de manera deliberada para que el modelo aprenda relaciones significativas entre las características en esa escala específica. Si cambias la escala en los datos de prueba, el modelo podría no funcionar de la misma manera y dar lugar a predicciones incorrectas.
4.- Reproducibilidad: Mantener los parámetros de escalamiento constantes entre el entrenamiento y la prueba permite que los resultados del modelo sean reproducibles y coherentes en diferentes momentos o en diferentes entornos.
Gracias por la aclaración!
Muy buen post! Lo único a resaltar es que la diferencia del error es muuucho mas grande. El mínimo error de los otros modelos es de ~$83k, con lo cual la diferencia es de ~$66k.