Material: Aritmética en la lógica
Clase 20 de 31 • Curso de Pensamiento Lógico 2018
Aritmética en la Lógica
Interpretación de los Números y Signos
La recta numérica es una recta en la que a cada uno de sus puntos le podemos asignar el valor de un número real.
Ley de los signos
Ejemplos:
Reto: Resolver las siguientes operaciones:
Razones y Proporciones Razón
Una razón es una comparación entre dos o más cantidades. Puede expresarse mediante una fracción. Si las cantidades a comparar son a y b, la razón entre ellas se escribe como:
Las razones se pueden amplificar y/o simplificar, y se mantiene la razón.
Ejemplos:
- Se realiza una encuesta a un grupo de estudiantes sobre “si practica algún deporte”. Luego de un análisis de las respuestas se concluye que 4 de cada 10 estudiantes practica algún deporte. R. La razón entre los estudiantes que practican deporte y el total de estudiantes es 4:10, que es equivalente a 2:5.
- El radio de la Luna es 3/11 del radio de la Tierra, y el radio del Sol es igual a 108 radios terrestres. Hallar la razón entre los radios de la Luna y del Sol.
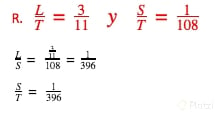
- En una sala de clases hay 10 mujeres y 18 hombres. ¿Qué relación numérica existe entre el número de mujeres y el número de hombres? R. La relación entre el número de mujeres y el número de hombres es de "10 es a 18" , otra forma de leerlo es "10 de 18 "
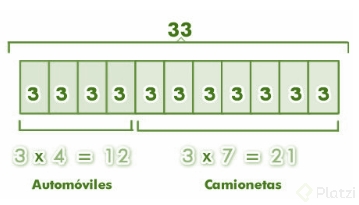
- Si hay 33 vehículos entre automóviles y camionetas y la razón entre ellos es 4:7 ¿cuántos automóviles hay?
En este caso se está comparando la cantidad de automóviles con el de camionetas. Para conocer la cantidad de automóviles que hay podemos seguir los siguientes pasos:
1° se considera el total de vehículos: 33
2° Se divide 33 por la suma entre el numerador y el denominador de nuestra razón (4+7= 11). Con esto se obtienen 11 partes con 3 unidades cada una (ya que 33:11 = 3).
3° Se consideran 4 partes para los automóviles y 7 para las camionetas.
R. Hay 12 automóviles.
Reto: Resuelve los siguientes problemas:
- Si la razón entre dos números es 2:3 y ambos suman 10 ¿Cuáles son los números? R. 4 y 6 4 y 6
- Martín tiene cinco fichas rojas por cada dos azules. Si tiene 21 fichas en total, entre rojas y azules, ¿Cuántas fichas tiene de cada color? R. 15 rojas y 6 azules
- A un taller de guitarra asisten 30 estudiantes. Si por cada 8 niñas hay 7 niños, ¿cuántos niños y niñas conforman el taller? R. 16 niñas y 14 niños
Proporción:
Una proporción es la igualdad de dos razones.
En toda proporción, el producto de los términos medios es igual al producto de los términos extremos (Teorema fundamental de las proporciones). Es decir:
Ejemplos:
-
En una tienda se venden dulces nacionales e importados, a razón de 3:2 Si sabemos que al día se vende 255 dulces nacionales, ¿Cuántos dulces importados se venden al día?
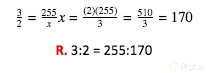
-
Dos grúas mueven 50 contenedores en hora y media. ¿Cuántas grúas se necesitan para mover los 50 contenedores en media hora?

Reto: Resolver los siguientes problemas.
- En una fiesta se invitaron a niños y niñas. Si sabemos que acudieron en una proporción de 6 niñas por cada 4 niños, y en la fiesta hay 32 niños ¿Cuántas niñas fueron? 6:4 = x:32 32 X 6 = 192 192 / 4 = 48 niñas fueron a la fiesta.
R. 6:4 = 48:32 (6 es a 4 como 48 es a 32)
- Si 4 alumnos realizan un trabajo en equipo en 45 minutos ¿Cuánto tiempo tardarán si el equipo está formado por 6, 8, 10 y 12 estudiantes? Tendremos las siguientes proporciones: a) 4:45 = 6:? b) 4:45 = 8:? c) 4:45 = 10:? d) 4:45 = 12:?
4 X 45 = 180
a) 180 / 6 = 30 minutos b) 180 / 8 = 22.5 minutos c) 180 / 10 = 18 minutos d) 180 / 12 = 15 minutos
Por lo que las proporciones serán:
a) 4:45 = 6:30 b) 4:45 = 8:22.5 c) 4:45 = 10:18 d) 4:45 = 12:15
Teorema de Tales
Antes de dar su enunciado, recordemos algunas nociones de semejanza de triángulos. Esencialmente, dos triángulos son semejantes si sus ángulos son congruentes (tienen la misma medida). Esto da lugar al hecho de que, si dos triángulos son semejantes, sus lados correspondientes (u homólogos) son proporcionales.
El primer teorema de Tales enuncia que si en un triángulo dado se traza una recta paralela a cualquiera de sus lados, el nuevo triángulo que se obtiene será semejante al triángulo inicial.
En la figura anterior, los triángulos ABC y DEC son semejantes.
Ejemplos:
-
Hallar el valor de x.

-
Las maderas de las repisas de la figura son paralelas. Calcula las longitudes de las maderas representadas como x e y.
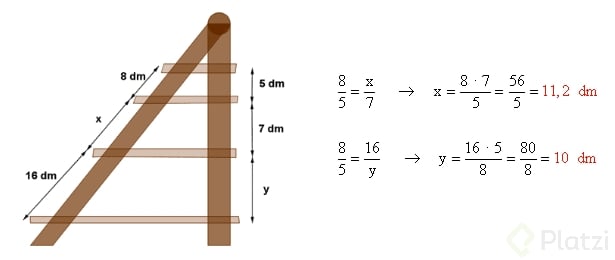
Reto: Resolver los siguientes problemas.
-
Hallar el valor de x.
: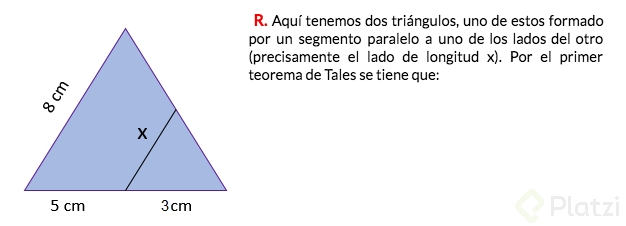
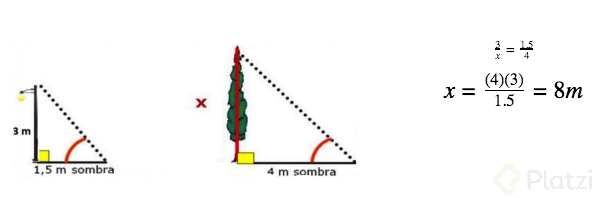
-
Un poste vertical de 3m proyecta una sombra de 1.5m, ¿Qué altura tendrá un árbol que a la misma hora proyecta una sombra de 4m?