Matemáticas de MLE (Clase 12)

Para un entendimiento profundo ver el tutorial del Andrés en: MLE

• Hola a todos. Este es un recuento de la clase 12 del curso. Es más que nada un repaso, y un poquito de poner las ecuaciones de manera explícita por si alguno tiene dudas del flujo que el profe Pacho hace en esta clase.

Estimación de Máxima Verosimilitud

Esencia

• Permite estimar densidades de probabilidad dentro de un esquema de trabajo general.

• Un subconjunto del estudio de la probailidad para estimar las densidades de probabilidad de un conjunto de datos.

Elementos

• Escoger distribución: Teniendo solo una muestra de datos.
• Escoger parámetros de la distribución: Que mejor ajustan la distribución a los datos.

Densidad de probabilidad

• En mi caso personal, describiría la estimación de máxima verosimilitud como la probabilidad máxima en que los datos se ajustan a un modelo. Si los datos son X y el modelo theta, se tiene la función que se quiere maximizar:

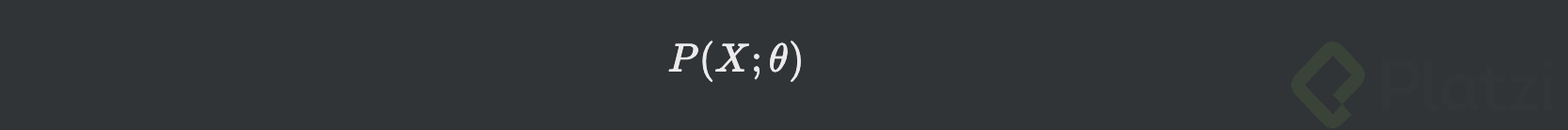
• Esto es, la probabilidad de que tus datos se ajusten al modelo. Para tener una nomenclatura más diciente, se nombra L (de likelihood) a la probabilidad en vez de P:

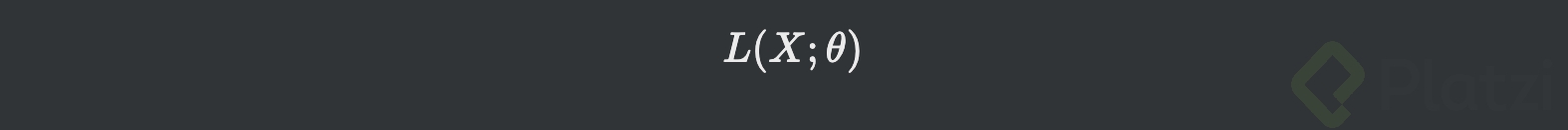
• Dado que X es un vector n-dimensional, se tiene:
  

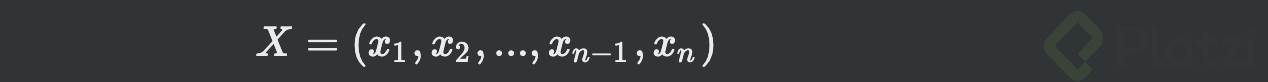
• Se puede escribir la probabilidad como:

• El conjunto de valores de X son conocidos. Se quiere saber la probabilidad de que esos valores ocurran para un parámetro desconocido theta. Sean los valores conocidos los números:

• Así pues podemos hacer más explícita la notación, diciendo que cada xi será igual a un valor conocido ai respectivo.

• Y dado que son probabilidades conjuntas, L se va a expresar como el producto de cada probabilidad:

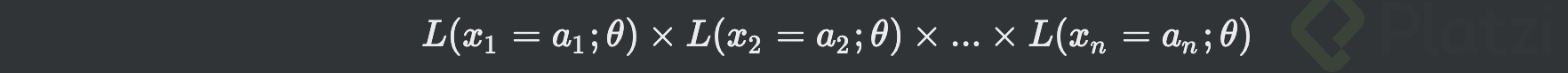
• Esto es, probabilidad que x1 sea el valor a1 y al tiempo x2 tenga el valor a2 y así sucesivamente; todos usando el mismo parámetro desconocido theta.

• Esto se puede escribir con la notación de productoria:

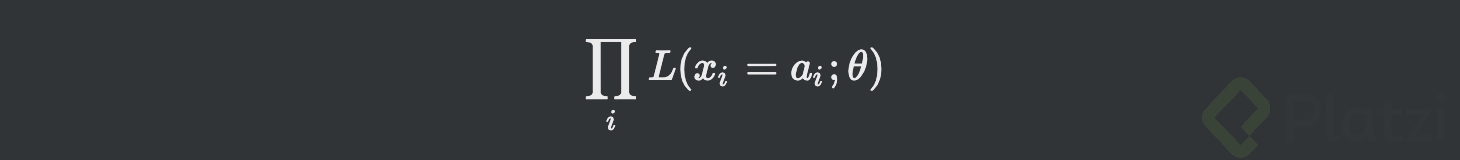
Tomar el logaritmo

• Como dice el profe Pacho, los valores de cada probabilidad están entre 0 y 1, fracciones propias. Por tanto al multiplicarlos obtienes números bastante pequeños, es decir con varios decimales en 0, del estilo: 0,00000x. Para solucionar esto, y a la vez aprovechar las propiedades matemáticas de los logaritmos se puede sacar el logaritmo a ambos lados de la ecuación:

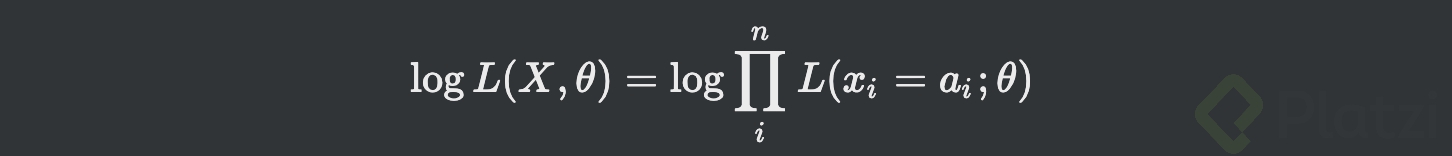
• El lado derecho de la ecuación da:

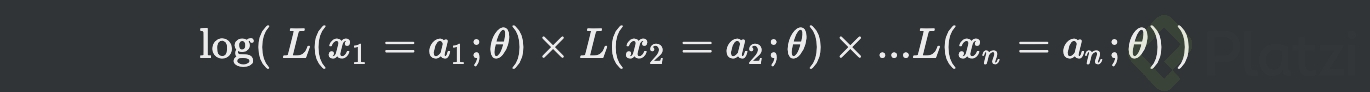
• Por propiedades:

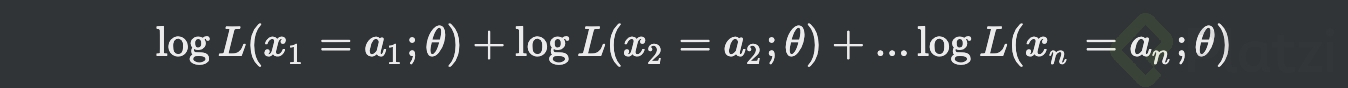
• Esto en notación de sumatoria queda:

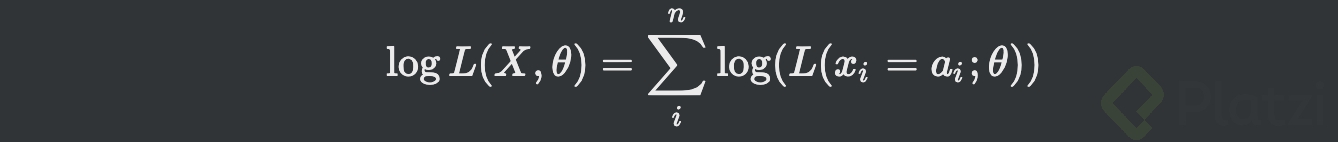
Maximización

• Lo último es que la función de máxima verosimilitud se obtiene a partir del máximo de esta función L, dado que estás tratando de hallar el máximo chance de que los datos sean ajustados a un modelo.

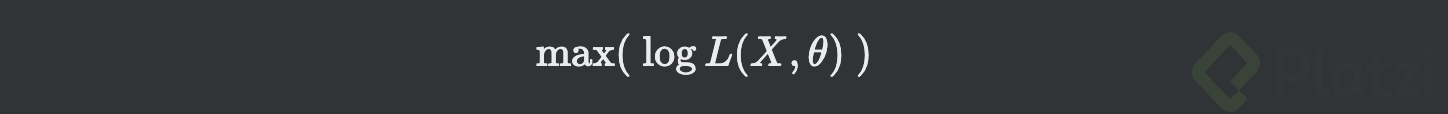
• Ó:

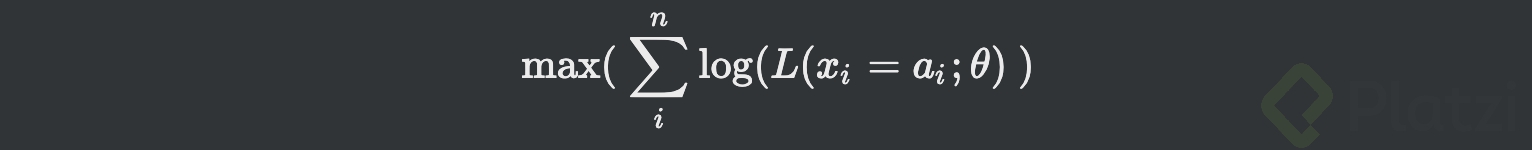
Cualquier duda o corrección es bienvenido : ) . Un saludo