Estadística de un jugador de fútbol:
Descriptiva: Resumir historial deportivo.
Inferencial: Predecir el desempeño del jugador.
¿Puedes mentir con estadística? sí.
¿Por qué aprender estadística?
Manera de resumir un conjunto de datos para extraer información valiosa.
Media (promedio).
Mediana (dato central).
Moda (dato que más se repite).
La tabla y diagrama de frecuencia se pueden usar.
¿Cuándo usar cual?
La media es susceptible a valores atípicos.
La moda no aplica para datos numéricos continuos.
Con esta metáfora vemos que no siempre la mediana es igual a la media. Esto sucede cuando existen outliers, como el sueldo de Bill Gates.
Numeró de comensales: 12
Sueldo de 11 comensales: 35000 USD.
Sueldo Bill Gates: 1000000 USD.
Media de sueldo: 115416 USD
Mediana de sueldo: 35000 USD
Histograma: para ver la distribución.
Dispersión en una distribución: Rango, rango intercuartil y desviación estándar.
Rango: valor máximo menos mínimo.
Rango intercuartil: subdivisión en 4 partes homogéneas.
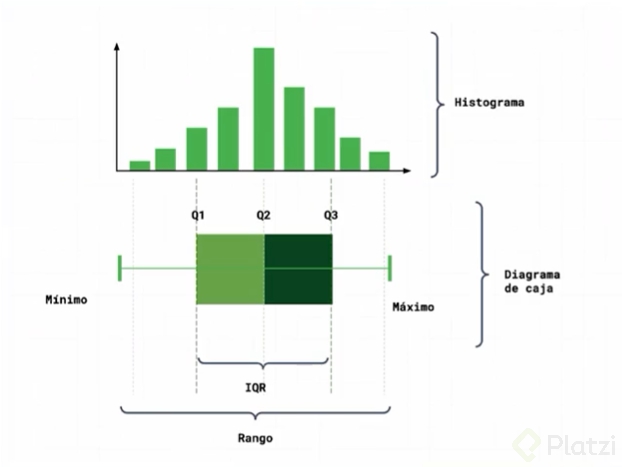
Se emplea para describir la distribución de los datos.
Funciona en datos que tienen una distribución normal.
En una distribución normal:
Se considera el 99.72% de los datos (6 sigma).
el valor mínimo es Q1 - 1.5IQR.
el valor máximo es Q3 + 1.5IQR.
Los valores fuera de los valores extremos no se tienen en cuenta.
Nota: Para distribuciones asimétricas los valore mínimos y máximos se hallan de manera diferente.
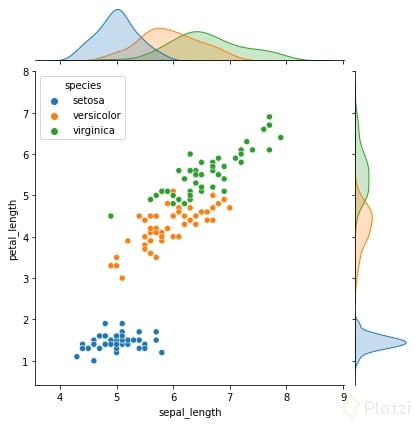
Un diagrama de dispersión nos permite encontrar la correlación entre dos variables.
Es necesario normalizar los datos antes de pasarlos por un modelo de machine learning, ya que estos son óptimos cuando los atributos están siempre en las mismas dimensiones.
Los modelos ML generalmente son eficientes en el rango [-1, 1].
Existen diferentes métodos para hacer este tipo de normalización o escalamiento:
Estos métodos se utilizan cuando se tienen distribuciones normales o gaussianas.
Cuando se tienen distribuciones no simétricas, antes de aplicarles algún método de escalamiento lineal, hay que aplicar una transformación no lineal.
Las transformaciones no lineales pueden ser:
Con esto podemos convertir variables categóricas en numéricas.
Puede ser
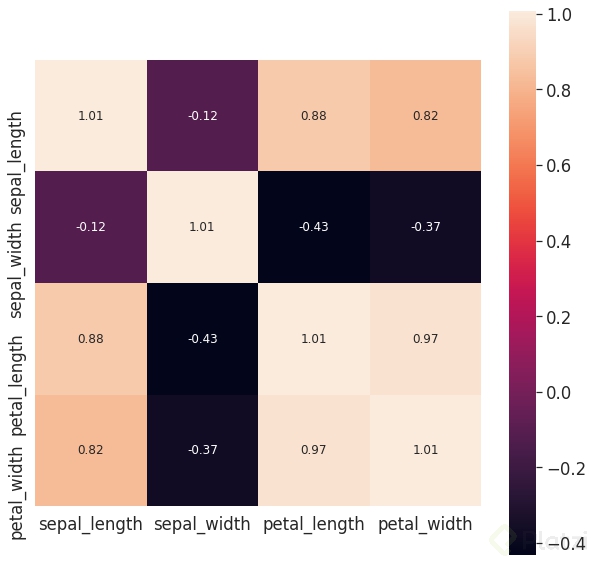
Cuando se hacen análisis de machine learning se puede reducir la cantidad de variables cuando algunas de estas presentan una fuerte correlación.
Cuando se miden correlaciones se usa la covarianza.
Otra manera más exacta de medir la correlación de dos variables es usando el coeficiente de correlación (rho).
Este coeficiente varía entre -1 y 1. Cuando es cercano a 0 la correlación es débil.
Cuando el coeficiente de correlación es cercano a 1 la correlación entre variables es directa.
Cuando el coeficiente de correlación es cercano a -1 la correlación entre variables es inversa.
Permite calcular todas las posibles relaciones de las variables de un dataset.
Nos permite por medio de los valores propios de la matriz de covarianza, identificar las direcciones a lo largo de las cuales se captura la mayor cantidad de varianza de los datos.
Con esto se pueden reducir el número de variables para facilitar el proceso con el modelo de machine learning.
Gracias Mauricio por el aporte