¿Cuál es la matemática detrás de la regresión lineal?

La regresión lineal es un modelo matemático que describe una relación lineal entre dos o más variables. Este modelo es útil para predecir valores numéricos y es uno de los algoritmos más sencillos y versátiles en el machine learning.

Como recordarás, y = b0 + b1x es la fórmula de una recta, donde b0 es el intercepto y b1 es la pendiente. De aquí partiremos para explicar la matemática detrás de la regresión lineal y cómo es que llegamos a obtener los valores de sus parámetros.

Así que te recomiendo haber tomado el Curso de Funciones Matemáticas para Data Science e Inteligencia Artificial para que comprendas el lenguaje matemático que viene a continuación.

Método de mínimos cuadrados y ajuste de curvas

Uno de los problemas a los que nos enfrentamos al ajustar una curva a los datos es encontrar sus parámetros óptimos. En el caso de regresión lineal estos son el intercepto b0 y la pendiente b1.

Para solucionarlo utilizamos una técnica que se llama ajuste por mínimos cuadrados. Esta consiste en minimizar la sumatoria del error entre el valor y real (observado) y el valor y de nuestro modelo de regresión.

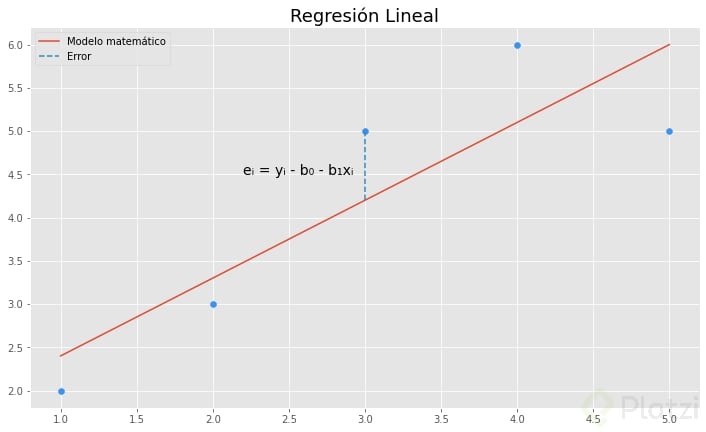
Observando la imagen, notamos que al error lo podemos representar con la siguiente ecuación:

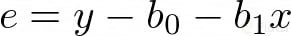
Teniendo en cuenta esto, procedemos a expresar matemáticamente el método de mínimos cuadrados:

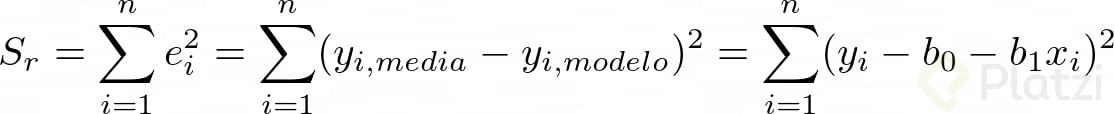
Para encontrar los valores de b0 y b1 derivamos la anterior expresión con respecto a cada una de estas variables:

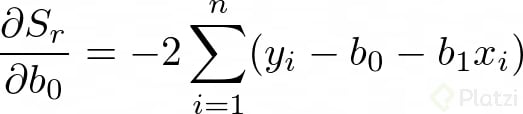
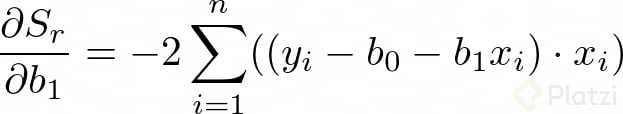
Dado que estamos buscando minimizar el error, igualamos las derivadas a cero. Vemos que ahora tenemos un problema de optimización. Recuerda que igualamos a cero las derivadas para encontrar un máximo o un mínimo. Así tenemos:

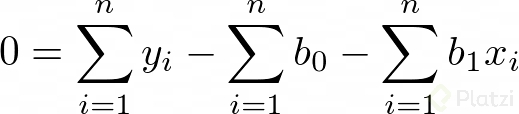
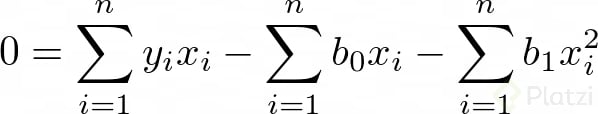
Luego, si consideramos que Σb0 = n*b0 (lo cual tiene sentido porque n es el número de datos), podemos expresar dos ecuaciones lineales de dos incógnitas:

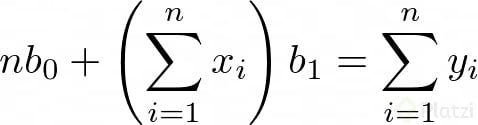
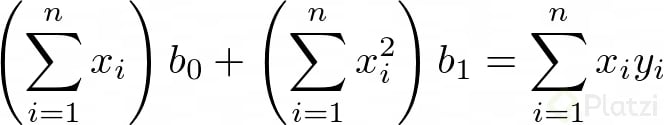
Ahora, si resolvemos para b0 y b1 obtenemos:

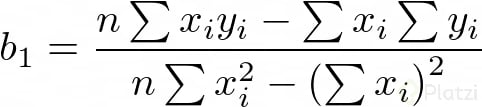
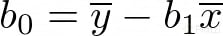
Donde ȳ y x̄ son las medias de x y y, respectivamente.

De esta forma hemos calculado los coeficientes b0 y b1 por el método de mínimos cuadrados. Ahora veremos la cuantificación del error, es decir, cuán erradas pueden ser nuestras predicciones.

¿Cómo cuantificar el error en la regresión lineal?

Cualquier otra línea (con diferentes parámetros) aumentaría el valor de la suma de los cuadrados de los residuos. Ergo, no sería la curva con mejor ajuste. Pero, ¿cómo es que medimos el error en la regresión lineal?

Consideremos que los datos siguen una distribución normal respecto a la línea de predicción y que el error es de magnitud similar a lo largo del data set. Esto se llama principio de máxima verosimilitud.

Para saber cuantificar el error debemos tomar en cuenta la suma total de los cuadrados de las diferencias entre los datos y la media St y la suma total de los cuadrados de las diferencias entre los datos y la curva de regresión Sr. Esto suena confuso, ¿no? Expresemos lo anterior en términos matemáticos para que quede más claro.

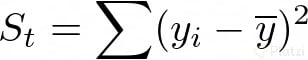
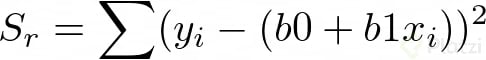
Ahora calculemos el error de aproximación entre estos dos valores, así:

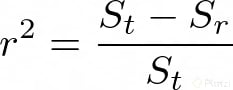
A r²se lo conoce como el coeficiente de determinación y a √(r²) como coeficiente de correlación. Entonces, cuando el coeficiente de correlación sea más cercano a 1 quiere decir que las predicciones serán menos erradas. En un caso ideal r será igual a 1, pero en el mundo real casi nunca te encontrarás con un caso así. Es muy raro.

Una forma más práctica de representar el coeficiente de correlación, desde el punto de vista computacional, es:

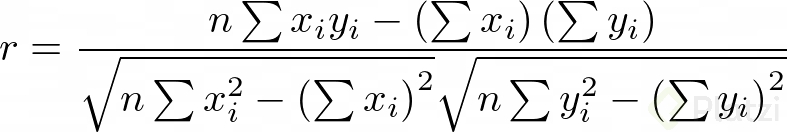
Y así es cómo cuantificamos el error y determinamos qué tan bien se ajusta el modelo matemático que creamos a los datos observados.

Entender los modelos te permite avanzar más rápido

¡Felicidades por llegar hasta aquí! Quizá te estés preguntando si debes aprenderte todas estas fórmulas para tener una carrera exitosa como data scientist. Pero la respuesta es NO. La idea de explorar los algoritmos desde un punto de vista lógico-matemático es entender lo que estamos haciendo y cómo podemos usarlo a nuestro favor.

Existen librerías de Python como Scikit-learn o SciPy que harán que tu trabajo sea más rápido y que no tengas que programar estas fórmulas. Y eso es lo correcto en un ambiente profesional. Sin embargo, lo que acabas de leer te permitirá avanzar más rápido e interpretar mejor tus modelos matemáticos.

Ahora ya sabes de dónde surge la regresión lineal. Espero que hayas disfrutado tanto esta lectura como yo disfruté de escribirla. Cuéntame en los comentarios si te gustaría que exploráramos algún otro modelo matemático.

Descubre más sobre: Matriz pseudoinversa de Moore Penrose.