Variables aleatorias y distribuciones de probabilidad que debes conocer

Quizá ya habrás escuchado de términos como distribución normal, distribución binomial, distribución de Poisson, etc. Y es que como data scientist serán parte de tu vocabulario cotidiano. Pero, ¿qué son exactamente? ¿Cuáles existen? Y más importante, ¿cómo las interpretamos?

Para los ejemplos que vamos a ver, he preparado un notebook para que puedas interactuar directamente con el código en Python. Por eso será muy útil que tengas conocimientos básicos en este lenguaje de programación. El Curso Básico de Python tiene lo que necesitas para entender el código de más adelante.

Dicho esto, empecemos por lo primero: variables aleatorias.

¿Qué es una variable aleatoria?

Podemos verla como el resultado de un experimento aleatorio. Por ejemplo, lanzar una moneda al aire. Los posibles resultados son cara o cruz, cada uno con el 50% de probabilidad de ocurrir. Pero no sabremos realmente el resultado hasta que el experimento (lanzar la moneda) sea realizado.

De esta manera, supongamos que lanzamos la moneda al aire 7 veces y obtenemos {H, H, T, H, T, T, T}. Esto será el resultado de nuestro experimento, donde H es cara y T es cruz. Antes de hacer el experimento no sabíamos que íbamos a obtener este resultado.

Ahora bien, las distribuciones probabilísticas son una manera de mapear esas variables aleatorias. Para seguir, vamos a diferenciar entre variables aleatorias discretas y variables aleatorias continuas.

Variables aleatorias discretas vs. continuas

Cuando hablamos de variables discretas nos referimos a aquellas que se pueden describir con valores finitos. Por ejemplo, lanzar una moneda solo tiene 2 posibles resultados: Cara o Cruz. Esto se puede traducir a 1 y 0 para hacerlo matemáticamente más manejable. Otro ejemplo es lanzar un dado. En este caso los ÚNICOS posibles resultados son 1, 2, 3, 4, 5, 6. No podemos obtener 1.3 o 3.72.

Por otra parte, las variables continuas pueden tomar valores infinitos. En este tipo tenemos, por ejemplo, la temperatura que podría tomar valores como 13, 13.5, 13.63, 14, etc. Entre 13 y 14 podríamos tener infinitos valores.

Teniendo esto claro, vamos a ver las distribuciones probabilísticas de este tipo de variables. Para esto utilizaremos un par de librerías de Python:

• NumPy para crear simulaciones probabilísticas.
• Matplotlib para graficar las distribuciones.

Aprovecho para recomendarte tomar el Curso Básico de Manipulación y Transformación de Datos con Pandas y NumPy y el Curso Básico de Visualización de Datos con Matplotlib y Seaborn para que tus habilidades con estas herramientas estén por las nubes.

Vamos entonces a importar nuestras librerías:

import numpy as np
import matplotlib.pyplot as plt

Distribución uniforme

Esta distribución aplica tanto para variables continuas como discretas. Básicamente, todos los eventos tienen la misma probabilidad de ocurrir. Por lo tanto, su gráfica será una curva uniforme y paralela al eje de las abscisas. Hacer simulaciones en Python es relativamente sencillo. Podemos simular así una distribución uniforme:

#Simulamos un experimento con 10000 muestras entre 0 y 6
uniform_samples = np.random.uniform(0, 6, size=10000)

fig, ax = plt.subplots()
plt.hist(uniform_samples, density=True, bins=6)
plt.title('Distribución uniforme', size=14)
plt.xlabel('Muestras')
plt.ylabel('Densidad')
plt.axhline(1/6, color='#3793ef', linestyle='--')
plt.show()

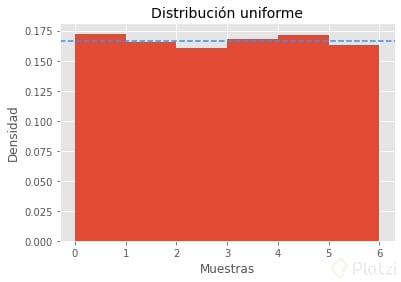
Como notarás, teóricamente, la probabilidad de ocurrencia de cada evento es 1/6, por eso he trazado una línea horizontal en ese valor. Si te preguntas la razón por la cual las muestras no están justo encima de esta línea, la respuesta es que hemos hecho una simulación, una aproximación numérica. No obstante, los valores son muy cercanos y podemos tomarlo como válido.

Nota también que el eje y muestra la densidad, es decir, la probabilidad de ocurrencia. No mostramos valores absolutos. Las gráficas de más adelante también serán así.

Distribución binomial

¿Recuerdas que al inicio de este artículo hablamos sobre un experimento de lanzar una moneda? Pues la distribución binomial mapea los resultados de hacerlo muchas veces. Primero tengamos en cuenta que lanzar una moneda una sola vez es un experimento de Bernoulli, en el que solo tienes 2 posibles resultados, cada uno con una probabilidad asociada. Los eventos son independientes.

Ahora, si repetimos varias veces el experimento de Bernoulli, tendremos una distribución binomial. Simulando esto en Python tenemos:

#Lanzamos una moneda 10 veces, esto lo repetimos 10000 veces. La probabilidad de éxito es 0.5
binomial_samples = np.random.binomial(10, 0.5, size=10000)

#Graficamos nuestra distribución 
fig, ax = plt.subplots()
plt.hist(binomial_samples, density=True, bins=11)
plt.title('Distribución binomial', size=14)
plt.xlabel('Muestras')
plt.ylabel('Densidad')
plt.axvline(10*0.5, color='#3793ef', linestyle='--')
plt.axvline(0, color='#3793ef', linestyle='--')
plt.axvline(10, color='#3793ef', linestyle='--')
plt.show()

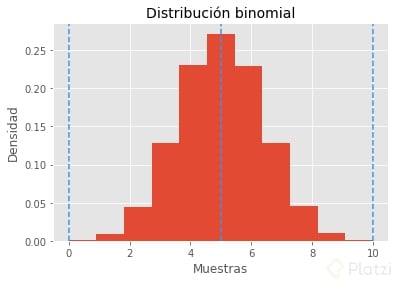
Vemos que la probabilidad máxima de ocurrencia está en el evento en el que p*n se cumple. Es decir, multiplicamos la probabilidad de éxito y el número de lanzamientos. Además, el rango de valores es igual al número de lanzamientos, en este caso, de 0 a 10.

Distribución de Poisson

Esta distribución de probabilidad discreta es ideal para expresar la probabilidad de que un número de eventos ocurra en un lapso de tiempo, siempre y cuando:

• Se conozca el tiempo promedio que pasa entre estos eventos.
• Los eventos sean independientes entre sí.

Por ejemplo, supongamos que en un partido de fútbol de 90 minutos el promedio de goles es 3. En Python, esto quedaría así:

#Hacemos una simulación de 10000 muestras
poisson_samples = np.random.poisson(3, 10000)

#Graficamos nuestra distribución
fig, ax = plt.subplots()
plt.hist(poisson_samples, density=True, bins=10)
plt.title('Distribución de Poisson', size=14)
plt.xlabel('Muestras')
plt.ylabel('Densidad')
plt.axvline(3, color='#3793ef', linestyle='--')
plt.show()

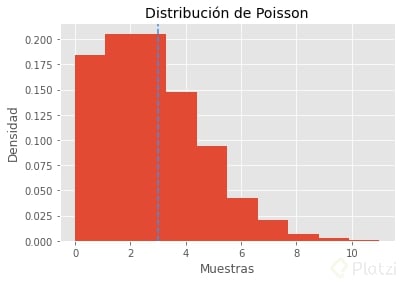
Como observas, aquí se llega al pico máximo en λ=3.

Distribución exponencial

Una vez tenemos una distribución de Poisson, ¿cómo hacemos para obtener una distribución del tiempo entre estos eventos? Es aquí que aplicamos una distribución exponencial. Tomando el ejemplo de los 3 goles por partido, en Python lo podríamos modelar así.

#Simulamos
exponential_samples = np.random.exponential(3, 10000)

#Graficamos
fig, ax = plt.subplots()
plt.hist(exponential_samples, density=True, bins=100)
plt.title('Distribución de exponencial', size=14)
plt.xlabel('Muestras')
plt.ylabel('Densidad')
plt.show()

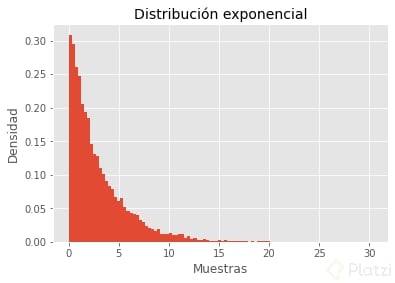
Nota que, mientras más partidos de fútbol ocurren, la probabilidad de que se marquen 3 goles tiende a ser del 100%. Recuerda que la probabilidad se obtiene por el área bajo la curva.

Distribución normal

A esta quizá ya la conocías. También se le llama distribución gaussiana. Y es que es la más comúnmente usada para modelar datos del mundo real. Pero ojo, eso no significa que sea el mejor enfoque que le podamos dar.

Los parámetros que necesitamos son la media y la desviación estándar. En Python podemos simularlo así:

#Generamos una muestra de 10000 elementos con media 0 y desviación estándar 1
normal_samples = np.random.normal(0, 1, size=10000)

#Graficamos nuestros datos
fig, ax = plt.subplots()
plt.hist(normal_samples, bins=50, density=True)
plt.title('Distribución normal', size=14)
plt.xlabel('Muestras')
plt.ylabel('Densidad')
plt.axvline(0, color='#3793ef', linestyle='--')
plt.axvline(np.std(normal_samples), color='#3793ef', linestyle='--')
plt.axvline(-1*np.std(normal_samples), color='#3793ef', linestyle='--')
plt.show()

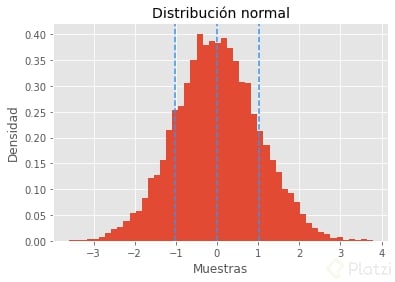
Como puedes observar, esta distribución tiene forma de campana, alcanza su pico en la media y su aplanamiento depende de la desviación estándar (kurtosis). Dado que es la distribución de una variable continua, tiene sentido analizar las probabilidades de ocurrencia por intervalos y no tanto por un solo valor. ¿Por qué?

• La probabilidad se puede obtener calculando el área bajo la curva, o sea, su integral.
• Al tener un rango, tenemos una base por una altura. Mientras que si tenemos un solo valor, tenemos solo altura. En teoría hay una base infinitesimal, pero esto tiende a cero.

Por eso se dice que la probabilidad de ocurrencia de 1 solo valor en una distribución de variables continuas es 0.

Las líneas verticales representan la desviación estándar (-1 y 1) y la media (0).

Cumulative distribution function

Si te fijaste bien, la probabilidad de ocurrencia de un valor o un rango de valores viene dada por el área bajo la curva. Y de tus clases del Curso Básico de Cálculo Diferencial para Data Science e Inteligencia Artificial recordarás que para obtener el valor de esa área tenemos que calcular la integral de la función, en este caso, de las distribuciones.

Pero aquí no haremos ningún cálculo tedioso, más bien, vamos a crear una función que nos servirá para futuros cálculos.

defecdf(data):"""Compute ECDF for a one-dimensional array of measurements."""# Number of data points: n
    n = len(data)

    # x-data for the ECDF: x
    x = np.sort(data)

    # y-data for the ECDF: y
    y = np.arange(1, n+1) / n

    return x, y

Entonces, si aplicamos esta función para la distribución normal, tendríamos algo así:

#Obtenemos los valores x e y
x_norm, y_norm = ecdf(normal_samples)

#Graficamos
fig, ax = plt.subplots()
plt.plot(x_norm, y_norm)
plt.title('ECDF de distribución normal', size=14)
plt.xlabel('Muestras')
plt.ylabel('Probabilidad acumulada')
plt.axvline(0, color='#3793ef', linestyle='--')
plt.axhline(0.5, color='#3793ef', linestyle='--')
plt.show()

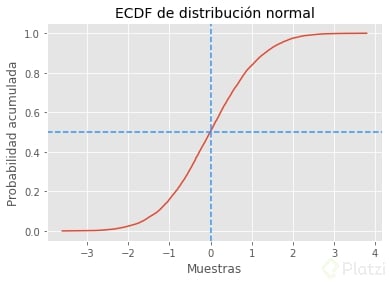
Ahora la gráfica representa la probabilidad de obtener un valor x o menor a este. Es decir, es una probabilidad acumulada. Como lo puedes observar, el 50% de porbabilidad acumulada está justo en la media de la muestra. Fíjate en la intersección de las líneas que he trazado.

Aplicamos la función a una distribución normal. Tu reto será hacerlo a una distribución exponencial e interpretarla. Puedes ver el resultado en la parte final del notebook que te compartí. 👀

Otras aplicaciones de las distribuciones probabilísticas

Quizá estés pensando que los ejemplos que acabas de leer son muy sencillos o son un cliché que aparecen en todos lados. Puede ser cierto. Pero es la base que necesitas comprender para realizar futuras simulaciones, experimentos y puedas interpretar correctamente los modelos de machine learning. Por eso, aquí te muestro algunas aplicaciones más avanzadas de las distribuciones probabilísticas y variables aleatorias.

• Climatología. La probabilidad de ocurrencia de un fenómeno natural como una lluvia fuerte o un tifón está determinada por estos modelos.
• Transporte. Teniendo datos históricos de accidentes de tránsito, se podría desarrollar un modelo para predecir cuántos accidentes habrá en cierto día. Y así, también reducirse.
• Procesamiento del lenguaje natural. Aquí se desarrolla un modelo estadístico de lenguaje sobre una secuencia de palabras para determinar el posible outcome.
• Test de hipótesis. Cuando se hacen estudios en poblaciones gigantes, por lo general se tiene únicamente acceso a una pequeña muestra de ellas. Es aquí que usamos distribuciones para encontrar significancia estadística.

¿Qué te ha parecido lo que acabas de leer? ¿Ha cambiado tu forma de ver las probabilidades? Recuerda que tener estos conceptos claros hará que avances mucho en tu carrera de data science. Cuéntame en los comentarios sobre los temas de que te interesaría aprender. Recuerda nuestra ruta de data scientist con python.