Las matemáticas son bellas por sí mismas, porque en ellas hay verdades universales. A lo largo de la historia de la humanidad se han formulado expresiones matemáticas que tienen un valor estético; ya sea por su precisión, descripción, formulación, profundidad o algún valor intrínseco que las hace únicas y bellas.
En el 2002, la matemática Natasha Kondratieva preguntó a un gran grupo de personas que estudiaban esa rama del saber cuáles consideraban las expresiones matemáticas más bellas. Allí hubo diversas opiniones, pero te hablaré de las 3 que fueron de las más mencionadas.
Teorema de Pitágoras
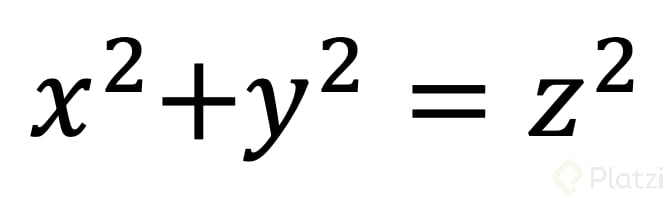
El teorema de Pitágoras hace referencia a un triángulo rectángulo donde z es la hipotenusa y las otras dos longitudes de sus lados son x y y. Es considerada una de las más bellas por estas particularidades:
- Intuitiva.
- Elegante y simple.
- Notación de potencias de variables.
- Une el álgebra y la geometría, formando la geometría analítica.
- Se demuestra sin palabras de manera simple, a través de geometría euclidiana.
- El teorema no es válido ante la geometría no euclidiana.
- Su generalización nos induce al teorema de Fermat.
Teorema de Euler para poliedros
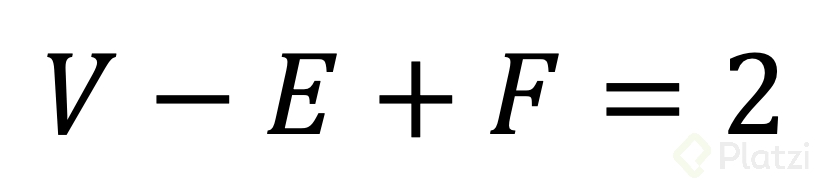
El teorema de Euler para poliedros dice que el número de vértices V de un poliedro, menos el número de sus aristas E, más el número de sus caras F, es igual a 2.
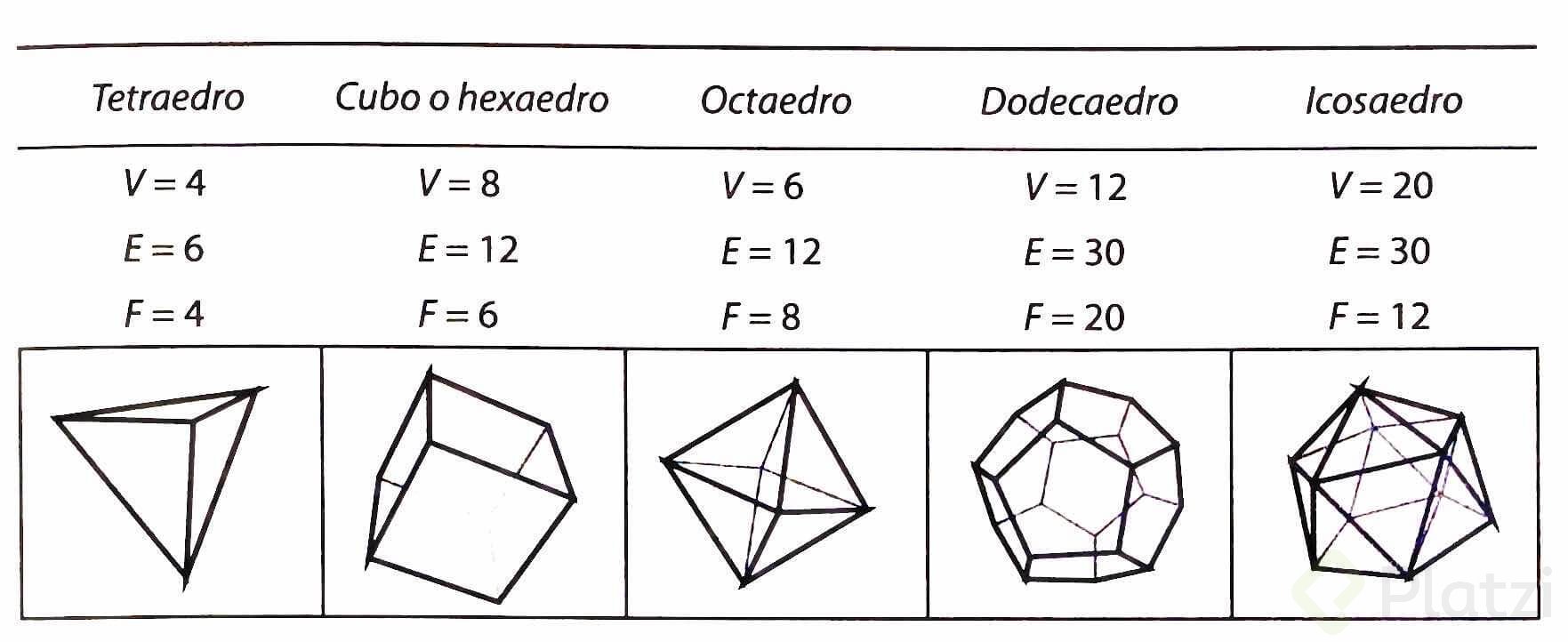
El mismo Euler al descubrir esta relación estaba muy emocionado, tanto que en 1750 le escribió a su amigo Christian Goldbach:
“Estoy sorprendido de que estas propiedades generales de la estereometría no hayan sido percibidas por nadie más, hasta donde estoy enterado.”
Identidad de Euler
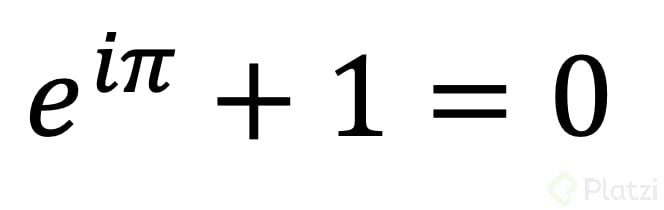
En la identidad de Euler tenemos la relación de la función exponencial con sus funciones trigonométricas con la generalización hacia el seno y coseno hiperbólico, esta identidad se estudia y la conocerás gráficamente a detalle en el Curso de Lenguaje y Notación Matemática que imparto, pero las principales características que la hace una de las expresiones más bellas son:
- Contiene al cero y al uno.
- Contiene el operador base de la suma.
- Incluye a dos números trascendentes e y π.
- Número imaginario i.
- Función exponencial con un número complejo.
Lo más impresionante es que su explicación gráfica vino después ya que Euler postuló la identidad de Euler en 1740, cincuenta años antes que Caspar Wessel desarrollara la representación de un número complejo como vector en un plano.
Aprende más sobre: Qué es la radicación y sus propiedades.
¡Te veo en mi curso para que puedas ver esta representación de manera gráfica y muchos temas más!
Curso de Lenguaje y Notación Matemática