- 1

Álgebra lineal: la base de la IA
01:33 - 2

Qué es un vector y cómo graficarlo
06:38 - 3

Suma, resta y multiplicación de vectores
12:56 - 4

Combinaciones lineales: construir planos con vectores
08:35 - 5

Independencia lineal: cuándo un vector es redundante
08:32 - 6

Producto punto: cómo medir alineación vectorial
09:20 - 7

Cómo calcular la norma de un vector
08:54 - 8

Ángulo exacto entre dos vectores con producto punto
08:04
Álgebra lineal: la base de la IA
Clase 1 de 29 • Curso de Álgebra Lineal: Fundamentos y Aplicaciones
Contenido del curso
- 14
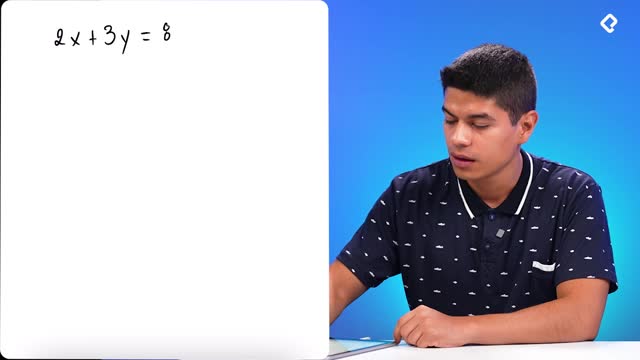
Sistemas de ecuaciones como Ax = b
06:55 - 15

Espacio columna vs espacio nulo en Ax=b
10:50 - 16
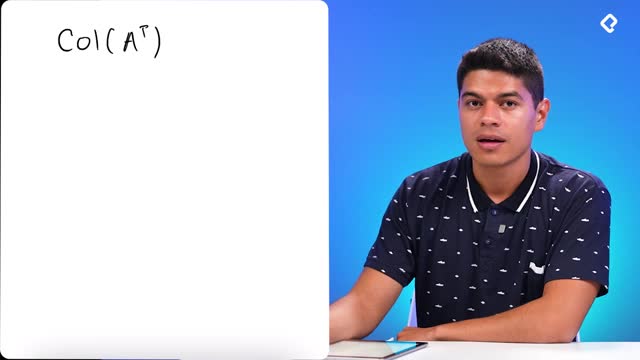
Ortogonalidad entre espacio fila y espacio nulo
05:32 - 17

Eliminación gaussiana paso a paso
11:48 - 18

Teorema rango-nulidad: conservación dimensional
09:18 - 19
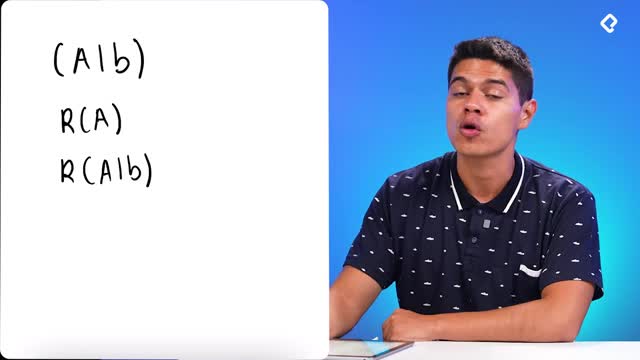
Diagnóstico de sistemas: rangos y tipos de solución
11:06 - 20

Proyección ortogonal: mejor aproximación cuando AX=b no tiene solución
10:50 - 21
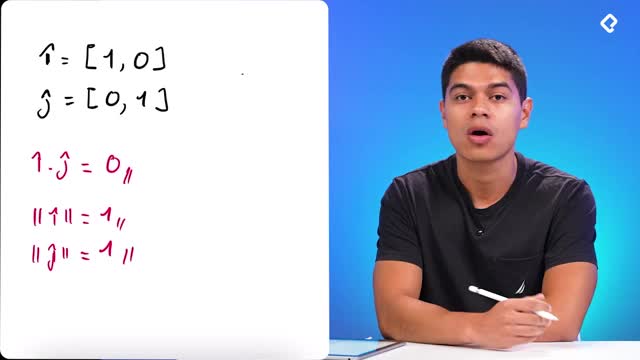
Gram-Schmidt: base torcida a ortonormal
14:11 - 22

Mínimos cuadrados para datos con ruido
16:10
La base de la inteligencia artificial, las simulaciones del clima, la robótica espacial y los videojuegos hiperrealistas es más clara de lo que parece: álgebra lineal. Este lenguaje matemático describe vectores, espacios n-dimensionales, matrices y transformaciones, permitiendo resolver sistemas de ecuaciones lineales a gran escala con precisión y eficiencia.
¿Por qué el álgebra lineal impulsa la tecnología actual?
El mensaje central es directo: debajo de tecnologías que parecen magia hay un conjunto de reglas que las vuelve comprensibles y calculables. Con esas reglas, un ingeniero modela fuerzas en un puente, un científico de datos encuentra patrones en millones de variables y un desarrollador rota objetos en 3D con naturalidad.
- IA que genera arte y código con estructuras lineales robustas.
- Simulaciones físicas que predicen el clima con miles de ecuaciones simultáneas.
- Robots que exploran Marte con modelos matemáticos confiables.
- Videojuegos hiperrealistas basados en transformaciones geométricas.
- Edificios que resisten terremotos gracias a modelado lineal.
¿Qué aprenderás con vectores, matrices y sistemas de ecuaciones?
El recorrido va de lo concreto a lo profundo: entenderás qué es un vector, cómo representar datos, operar con ellos y transformarlos con matrices. Dominarás la resolución de sistemas de ecuaciones lineales y, cuando no exista solución exacta, obtendrás la mejor aproximación posible.
¿Cómo representan datos los vectores?
- Flechas con tamaño y dirección para describir objetos.
- Puntos en espacios n-dimensionales que condensan características.
- Operaciones básicas: suma, escalar, combinación lineal.
¿Cómo transforman las matrices?
- Aplican rotaciones, escalados y proyecciones entre espacios.
- Describen transformaciones lineales que preservan estructura.
- Permiten componer efectos complejos de forma sistemática.
¿Cómo se resuelven sistemas y se aproxima cuando no hay solución exacta?
- Método para resolver sistemas lineales de muchas ecuaciones.
- Criterio para detectar cuando no hay solución única.
- Estrategia para calcular la mejor aproximación y reducir error.
¿Qué revelan inversa, determinante y eigenvalores sobre las transformaciones?
Al analizar la estructura profunda, aprenderás a deshacer una transformación con la inversa, a medir su impacto con el determinante y a identificar sus ejes naturales con eigenvalores y eigenvectores. Así entenderás qué cambios son recuperables, cuánta “escala” aplican y en qué direcciones actúan con mayor fuerza.
- Inversa: devuelve al estado original si la transformación es reversible.
- Determinante: cuantifica cambio de área/volumen y detecta colapsos.
- Eigenvalores y eigenvectores: ejes propios que simplifican el análisis.
Profesor: Daniel Erazo, ingeniero de software especializado en inteligencia artificial, te guía para comprender el lenguaje que construye el presente y el futuro.
¿Tienes alguna duda o ejemplo que quieras conectar con vectores o matrices? Compártelo en los comentarios y conversemos.