¿Qué es la probabilidad?, ¿Cuales son sus leyes? y como podemos implementarla en ejemplos practicos

Este pequeño tutorial forma parte de mis apuntes 📝 de la clase de Cálculo de Probabilidades
La probabilidad es un cálculo matemático que establece todas las posibilidades de que un evento ocurra en circunstancias donde interviene el azar (elementos aleatorios).

El valor de la probabilidad se encuentra ente el 0 y 1, donde:

• 0 = Imposible que el evento ocurra.
• 1 = Es seguro que el evento ocurra.

Formula de la probabilidad:

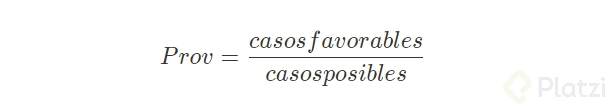
Calcular todas las posibilidades de un evento para entender su probabilidad, nos lleva a responder a la pregunta ¿Qué fracción de todos los posibles eventos tiene la propiedad que buscamos?.

La probabilidad de que un evento suceda o no suceda siempre es 1 (al sumar ambas probabilidades), a esto se le llama “Ley del complemento”.

Ley del complemento

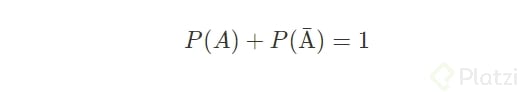
Esta ley (o regla) dice que si tenemos un evento A y su evento complementario(contrario) ~A entonces se cumple que
P(~A) = 1 - P(A)

Expresado de otra forma sería “la probabilidad de que no ocurra A es igual a 1 menos la probabilidad de que si ocurra A

Un ejemplo claro, si lanzamos un dado de 6 caras, la probabilidad de que salga 1 es de 1/6, la probabilidad de que no salga 1 es de 5/6, si sumamos ambas probabilidades nos da como resultado 6/6 = 1

El evento A es que el dado caiga en 1, y el evento contrario **~A **es que no caiga 1, por lo tanto tenemos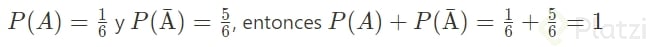

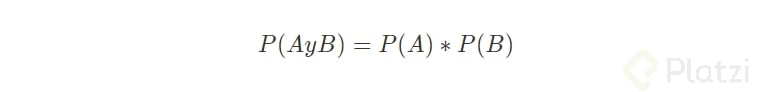
Ley multiplicativa

Esta ley permite encontrar la probabilidad de que un evento A y un evento B ocurran al mimos tiempo (probabilidad conjunta).

Esta regla depende de si los eventos son dependientes o independientes entre si.

• Dependientes: Cuando la ocurrencia de uno de los eventos depende de la ocurrencia del otro.
• Independientes: Cuando la ocurrencia de uno de ellos no afecta en la ocurrencia del otro, cuando A y B no están relacionados

Ley aditiva

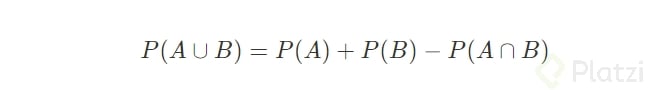
Esta ley establece que si tenemos un evento A y un evento B, la probabilidad de que ocurra el evento A o el evento B se calcula de la siguiente forma:

• P(A) : Probabilidad de que el evento A ocurra
• P(B): Probabilidad de que el evento B ocurra
• P(A o B) : Probabilidad de que ocurra el evento A o el evento B
• P(A y B) : Probabilidad de que los eventos A y B ocurran a la vez

Lanzamiento del dado

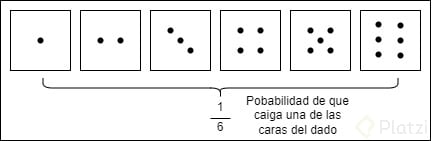
Utilizando las leyes anteriores podemos hacer preguntas concretas de probabilidad en este ejemplo de lanzamiento del dato, partiendo de la base de que la probabilidad de que una cara caiga en un lanzamiento del dado es de 1/6 (recordando que la probabilidad se calcula como casos favorables/casos posibles), podemos responder las siguientes preguntas:

1. ¿Cuál es la probabilidad de que salga 1? R: 1/6
2. ¿Cuál es la probabilidad de que salga 1 ó 2?
   En este ejemplo podemos utilizar la ley aditiva, donde el evento A=Cara con 1, evento B= Cara con 2, entonces tendríamos :
   
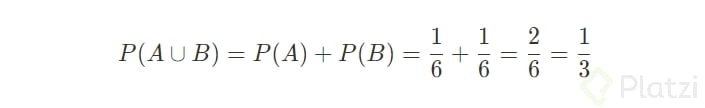
   Por lo tanto, la probabilidad de obtener 1 ó 2 al lanzar el dado es de1/3 que equivale a 0.333…
3. ¿Cuál es la probabilidad de NO obtener 1?
   Para contestar a esta pregunta implementaremos la ley del complemento P(~A) = 1-P(A)
   Donde 1 representa todas las posibilidades y P(A) probabilidad del evento que no queremos obtener. Tendríamos lo siguiente: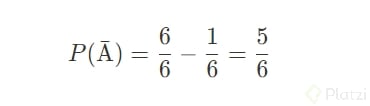
   
   Por lo tanto las probabilidades de no obtener 1 al lanzar el dado es de 5/6 que equivale a 0.833…
4. ¿Cuál es la probabilidad de NO obtener un 1 en 10 lanzamientos del dado?
   Partiendo de la respuesta a la pregunta anterior, donde la probabilidad de no obtener un 1 es de 5/6 en un lanzamiento, y utilizando la ley multiplicativa donde cada evento corresponde a dicha probabilidad y el número total de eventos es 10 (veces que se lanzará el dado), tendríamos lo siguiente: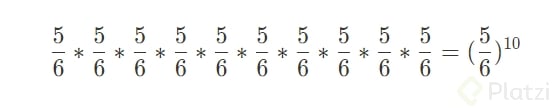
   
   Por lo tanto la probabilidad de que en 10 lanzamientos no salga el 1 es de (5/6)^10 que equivale más ó menos a 0.1615…
   .
   📓 Este tipo de ejemplos se resolvieron de forma analítica a punta de lápiz y papel, un punto importante a destacar es que entre más lanzamientos del dado queramos hacer o bien si queremos contestar preguntas más complejas, esta forma se vuelve ineficiente, sin embargo existen otras herramientas que nos ayudan a resolverlo de forma rápida y menos tediosa, una de ellas es la simulación.
   .
   Made with 💚 by Paho!