Guía definitiva para dominar NumPy

En esta guía aprenderás qué es NumPy, por qué usarlo y un tutorial paso a paso para que domines todos los conceptos fundamentales y empieces a usarlo ya mismo en tu día a día. Además, te esperan varios regalos y recursos extra 🎁

¿Qué es NumPy?

NumPy (Numerical Python) es una librería numérica de Python, de código abierto, que proporciona estructuras de datos matriciales y funciones matemáticas de alto nivel. Si te quieres dedicar a la ciencia de datos, estás siguiendo una ingeniería o algo relacionado con matemáticas, NumPy será la base de todo lo que hagas.

Cómo instalar NumPy

Si vas a trabajar con Notebooks en la nube, NumPy ya estará instalado. Pero si vas a trabajar en local, puedes instalarla desde la consola en tu máquina directamente o en un ambiente virtual de la siguiente manera:

pip install numpy

Por convención, se importa a Python de esta manera:

import numpy as np

¿Por qué usar NumPy?

Tiene una estructura de datos especial que te permite representar elementos complejos como imágenes, videos, canciones, modelos 3D, etc. Si tienes datos por procesar, NumPy será tu mejor amigo. Además, podrás realizar operaciones numéricas de manera muy sencilla, ahorrándote tener que programar ciclos o cosas extrañas.

A simple vista podrá parecer que con las listas de Python es posible hacer las mismas cosas que con NumPy, pero hay 3 grandes diferencias:

1. Las estructuras de datos de NumPy ocupan menos espacio en memoria que las listas.
2. También son significativamente más rápidas. Esto es porque NumPy está escrito en su mayor parte en C. Así que es tu aliado para lidiar con grandes cantidades de datos.
3. En NumPy ya están realizadas muchas funciones que en Python tendríamos que programar con ciclos y dominando muchos conceptos matemáticos.

Pero eso no es todo, varias de las grandes librerías de Python para Data Science, como Pandas, están escritas sobre NumPy y lo potencian. De hecho NumPy es la base de SciPy.

Tus primeros pasos con NumPy

Antes de iniciar, duplica (o descarga) un Notebook que preparé con todo lo que veremos en este tutorial y ejercicios adicionales para que puedas ir ejecutando y modificando todos los bloques de código en tu propia cuenta de Deepnote:

Descargar notebook del tutorial de NumPy

Ahora sí, ¡empecemos!

Arrays de NumPy

En NumPy se trabaja con una estructura de datos llamada array o arreglos numéricos multidimensionales. Los arrays son parecidos a las listas de Python, por ejemplo, heredan algunas propiedades como el ser mutables y poder realizar slicing (de hecho podemos crear un array a partir de una lista). Pero tienen diferencias importantes: son menos pesados, más rápidos y permiten crear fácilmente arrays n-dimensionales.

¿N-dimensionales? ¿Qué significa eso? 🤔 Bueno, vamos a darles nombres y una grafiquita para que quede más claro. Un array unidimensional puede ser una fila o una columna de una tabla (sí, igual que una lista), esta se conoce como vector. Un array bidimensional es lo que llamamos comúnmente matriz. Y un array de 3 dimensiones (o más), es decir, una matriz de matrices, se conoce como tensor.

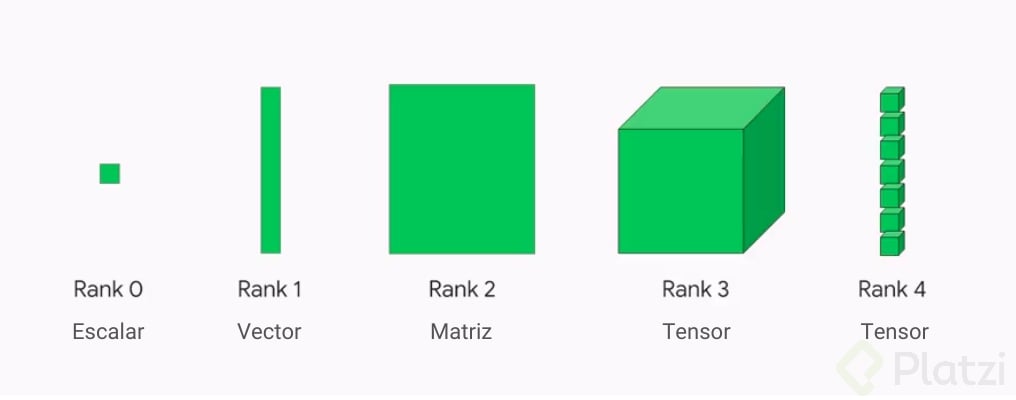
Pero… ¿Cómo se ve esto en código? (Ignora cómo lo construí, más adelante te enseñaré a hacerlo)

>>> vector = np.arange(5)
>>> vector
array([0, 1, 2, 3, 4])

>>> matrix = np.arange(9).reshape(3, 3)
>>> matrix
array([[0, 1, 2],
       [3, 4, 5],
       [6, 7, 8]])

>>> tensor = np.arange(12).reshape(3, 2, 2)
>>> tensor
array([[[ 0,  1],
        [ 2,  3]],

       [[ 4,  5],
        [ 6,  7]],

       [[ 8,  9],
        [10, 11]]])

💡 Algo muy importante que tienes que saber es que los arrays tienen que tener un único tipo de dato. Esto hace que sea muy eficiente almacenarlos y acceder a ellos. Si intentas poner varios tipos de datos, NumPy te cambiará algunos elementos para que todos sean homogéneos. Por ejemplo, si creas un array con strings y enteros, te los transformará para que todos sean strings o si pones enteros y flotantes, hará que todos sean flotantes.

Y una última regla: el tamaño de tus arrays 2D+ tiene que ser “rectangular”. Esto es igual que en matemáticas, si tu primera columna tiene 4 elementos, todas las columnas deberán tener 4 elementos. Lo mismo aplica para las filas.

¿Cómo crear un array en NumPy?

Como ya lo mencioné, se puede crear un array a partir de una lista o una lista de listas. Así que la forma más directa de crearlo es con np.array(tu_lista). Y al igual que las listas, puedes acceder a sus valores por medio de sus índices.

>>> my_first_vector = np.array([2, 5, 6, 23])
>>> print(my_first_vector)
[ 25623]

>>> my_first_matrix = np.array([[2, 4,], [6, 8]])
>>> print(my_first_matrix)
[[24]
 [68]]

>>> my_list = [0, 1, 2, 3, 4]
>>> print(np.array(my_list))
[01234]

Creando arrays secuenciales con arange y linspace

También puedes crear arrays con secuencias de números. Te mostraré 2 maneras de hacerlo.

np.arange()

Funciona parecido a range en Python, solo que en lugar de regresar un generador, retorna un ndarray. Sus argumentos principales son: start, stop y step. Con lo que puedes dar un rango de valores y cada cuánto quieres que aparezcan.

Toma en cuenta que start es inclusivo y stop es exclusivo. Igual que al hacer slicing en una lista.

>>> print(np.arange(start=2, stop=10, step=2))
[2468]

>>> print(np.arange(11, 1, -2))
[119753]

np.linspace()

Con np.arange() puedes decir cada cuánto quieres que genere los elementos y con ello te dará un tamaño de array. En cambio con np.linspace() puedes decir el tamaño del array (num) y los steps se calcularán automáticamente. Y aquí tanto start como stop son inclusivos.

>>> print(np.linspace(start=11, stop=12, num=18))
[11.11.0588235311.1176470611.1764705911.2352941211.2941176511.3529411811.4117647111.4705882411.5294117611.5882352911.6470588211.7058823511.7647058811.8235294111.8823529411.9411764712.        ]

>>> print(np.linspace(0, 1, 11))
[0.0.10.20.30.40.50.60.70.80.91. ]

Creando arrays vacíos y predefinidos

Es posible que necesites crear arreglos “vacíos” o con valores pre-definidos. Para ello hay 3 funciones muy útiles:

np.zeros() y np.ones()

Ambas funciones te permiten crear arrays llenos de 0 o 1 según corresponda. Toma en cuenta que si quieres crear más de una dimensión, deberás pasarlo en una tupla.

>>> print(np.zeros(4))
[0.0.0.0.]

>>> print(np.zeros((2, 2)))
[[0.0.]
 [0.0.]]

>>> print(np.ones(6))
[1.1.1.1.1.1.]

np.full()

Crea un array con un valor en específico. Tiene 2 argumentos principales: shape que tiene que ser pasado como una tupla con las dimensiones y fill_value con el valor que desees.

>>> print(np.full(shape=(2, 2), fill_value=5))
[[55]
 [55]]

>>> print(np.full((2, 3, 4), 0.55))
[[[0.550.550.550.55]
  [0.550.550.550.55]
  [0.550.550.550.55]]

 [[0.550.550.550.55]
  [0.550.550.550.55]
  [0.550.550.550.55]]]

np.full_like()

Sirve si ya tienes un array creado y quieres tomarlo como base para crear otro con el mismo tamaño, pero con un mismo valor.

>>> base = np.linspace(2, 6, 4)
>>> print(np.full_like(base, np.pi))
[3.141592653.141592653.141592653.14159265]

Arreglos aleatorios

Si quieres generar una serie de números totalmente aleatoria, ¡lo puedes hacer! Pero no solo eso, sino que si quieres que esos números obedezcan una distribución, puedes indicarlo. Para ello deberás usar np.random. Veamos algunas funciones que te pueden ayudar.

• .rand(): números aleatorios en una distribución uniforme. Permite crear ndarrays.
• .uniform(): parecido a rand, pero permite ingresar los límites de la muestra.
• .randn(): números aleatorios en una distribución normal. Permite crear ndarrays.
• .normal(): parecido a randn, pero permite escalar los límites de la muestra.
• .randint(): números enteros aleatorios entre un rango dado.

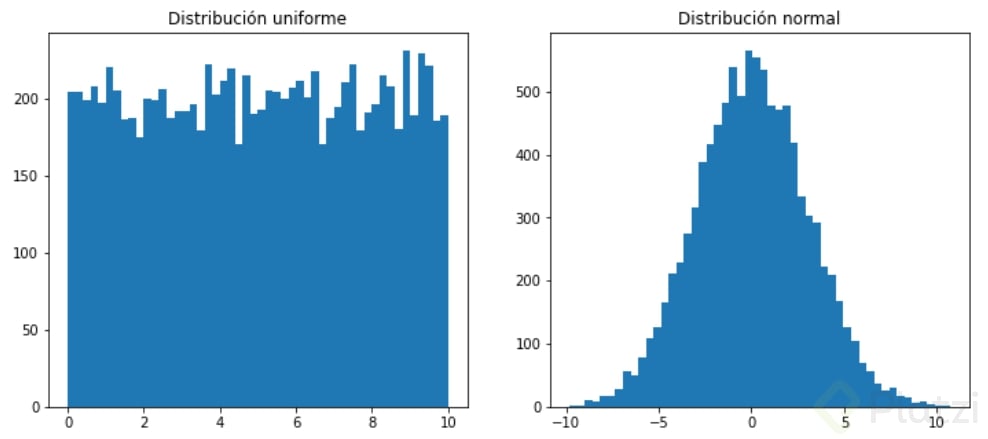
>>> print(np.random.rand(2, 2))
[[0.394491720.53571876]
 [0.022215650.74657571]]

>>> print(np.random.uniform(low=0, high=1, size=6))
[0.130789890.343159910.775262170.242149040.692140140.25820501]

>>> print(np.random.randn(2, 2))
[[-0.23459831-1.62879852]
 [-1.77888446-1.09441255]]

>>> print(np.random.normal(loc=0, scale=2, size=6))
[ 1.62808825-2.001851681.70594920.78900208-0.927127490.1071917 ]

>>> print(np.random.randint(low=0, high=10, size=(3, 3)))
[[203]
 [771]
 [412]]

Retos:

• Crea un tensor 3D a partir de listas.
• Crea un array con 100 valores entre 6 y 9.
• Haz que el anterior array ahora tenga todos sus valores iguales a pi.
• Crea un array 1D de 10000 números aleatorios.

Tamaño de los arrays

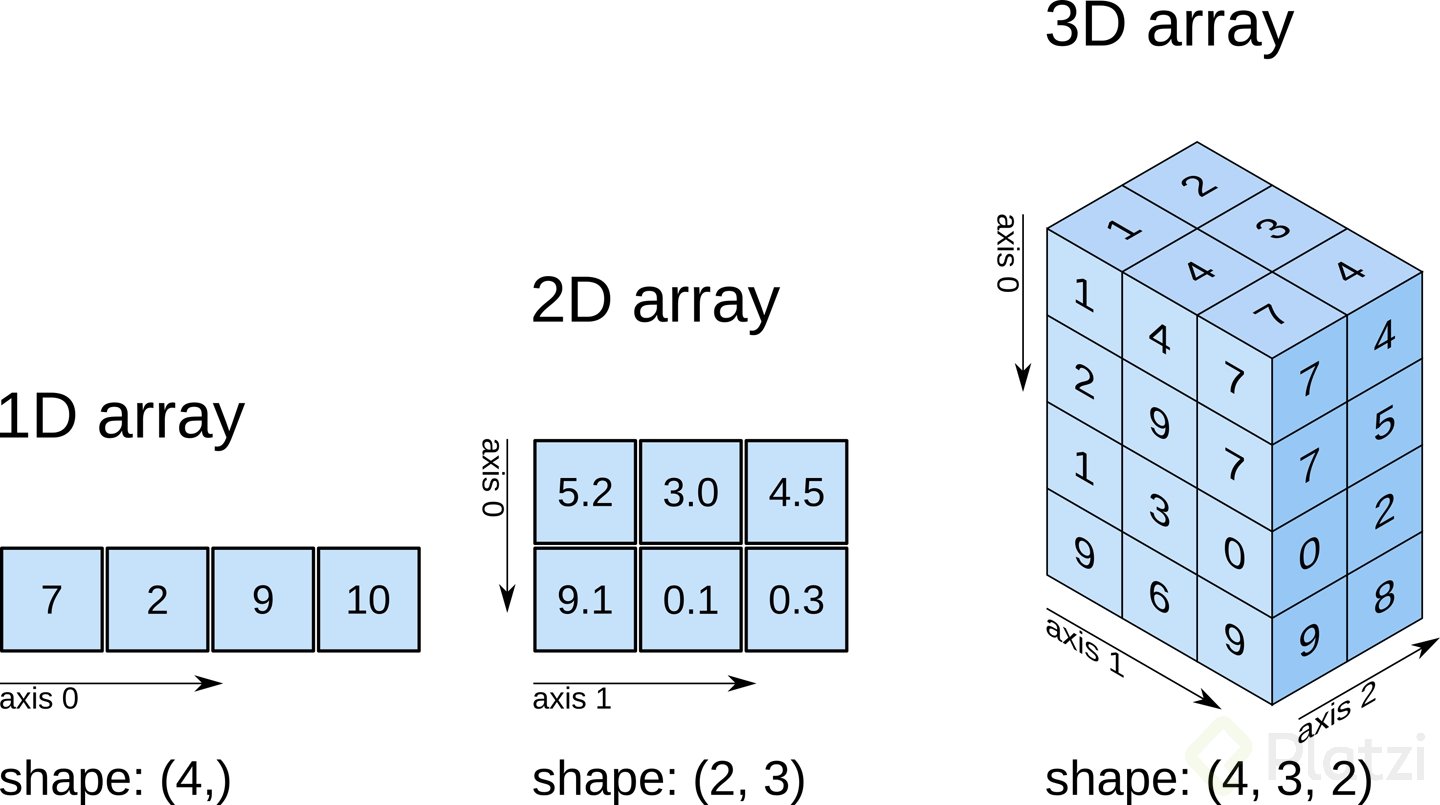
Hay un par de funciones y métodos que te ayudarán a saber las dimensiones que un array y su tipo de datos:

• .shape: devuelve las dimensiones del array. Para una matriz el primer valor son las filas y el segundo las columnas. Para un tensor el primer valor es la “profundidad”, el segundo las filas y el tercero las columnas.
• .reshape(): redimensiona un array, es decir, te permite crear matrices o tensores a partir de vectores y viceversa. También funciona como método.
• .dtype: devuelve el tipo de dato de un array.

>>> C = np.arange(1, 9).reshape(2, 2, 2)
print(C)
[[[12]
  [34]]

 [[56]
  [78]]]

>>> a = np.arange(1,10)
>>> B = np.reshape(a, [3,3])
>>> print(B)
[[123]
 [456]
 [789]]

>>> print(B.shape)
(3, 3)

>>> print(B.dtype)
int64

Reto:

• Intenta crear un array con diferentes tipos de datos (por ejemplo, enteros y flotantes). ¿Si usas .dtype(), qué tipo de dato es?
• Crea una matriz de 10 × 10 a partir de un vector secuencial (analiza cuál es la mejor solución, usar np.arange o np.linspace).

Manipulando arrays

Es hora de manipular los arrays. De manera muy parecida a las listas, los ndarrays permiten hacer slicing con la notación [filas, columnas] y sus índices inician en 0.

Se puede hacer slicing con esta notación [2:5, 3:6]. Para seleccionar toda una columna o fila, se usa :. Por ejemplo:

• [1, :] ← esto selecciona todas las columnas de la segunda fila.
• [:, 2] ← esto selecciona todas las filas de la tercera columna.

Veamos algunos ejemplos con una matriz para que quede más claro.

>>> matrix_cool = np.arange(9).reshape(3, 3)
>>> print(matrix_cool)
[[012]
 [345]
 [678]]

>>> print(matrix_cool[1, 2])
5>>> print(matrix_cool[0, :])
[012]

>>> print(matrix_cool[:, 1])
[147]

>>> print(matrix_cool[:, 1:])
[[12]
 [45]
 [78]]

>>> print(matrix_cool[0:2, 0:2])
[[01]
 [34]]

>>> print(matrix_cool[:, :])
[[012]
 [345]
 [678]]

Retos

• Crea una matriz de 10 × 10 y accede a sus columnas 4, 5 y 6 y a sus filas 8 y 9.
• Selecciona solo la fila 2.
• Crea un tensor de 2 × 10 × 10 e intenta replicar el ejercicio para la segunda matriz. ¿Qué tuviste que hacer diferente?

Copiar un array de NumPy

Al ser mutables, para copiar un ndarray lo mejor es usar array1.copy() o nuevamente np.array(array1).

❌ Incorrecto

>>> a1 = np.array([2, 4, 6])
>>> a2 = a1
>>> a1[0] = 8>>> print(a1)
[846]
>>> print(a2)
[846]

✅ Correcto

>>> a1 = np.array([2, 4, 6])
>>> a2 = a1.copy()
>>> a1[0] = 8>>> print(a1)
[846]
>>> print(a2)
[246]

Funciones matemáticas

¡Has aprendido un montón hasta ahora! Así que vamos a terminar revisando un poco sobre las posibilidades que nos da NumPy con las operaciones matemáticas.

Empecemos con la suma y resta. Si intentas sumar dos listas, se van a concatenar. Pero si intentas sumar 2 ndarrays del mismo tamaño, se sumaran cada uno de sus elementos entre sí sin problemas, al igual que hacer una suma de matrices.

>>> A = np.arange(5, 11)
>>> print(A)
[ 5678910]
>>> print(A + 10)
[151617181920]

>>> B = np.full(4, 3)
>>> C = np.ones(4, dtype='int')
>>> print(B)
[3333]
>>> print(C)
[1111]
>>> print(B - C)
[2222]

Con la multiplicación y división las cosas se ponen un poco más complejas. Si tienes una matriz y la multiplicas o divides por un escalar, las operaciones se aplicarán de manera muy similar que lo que vimos con la suma.

Pero si intentas multiplicar una matriz y un vector o dos matrices, las reglas cambian, y se aplica algo llamado broadcasting y aparecen operaciones como el producto punto. Con NumPy es extremadamente sencillo aplicarlo, pero debes tener claro los conceptos matemáticos detrás de ello. No te preocupes, más adelante hablaré de eso, ahora veamos operaciones básicas.

>>> print(A * 10)
[ 5060708090100]

>>> print(A / 10)
[0.50.60.70.80.91. ]

Algo muy útil que seguramente usarás en el día a día es la estadística. Para obtener valores como la media, mediana o desviación estándar. Solo necesitas un array con tus datos y NumPy hará el resto por ti.

>>> height_list = [74, 74, 72, 72, 73, 69, 69, 71, 76, 71, 73, 73, 74, 74, 69, 70, 73, 75, 78, 79, 76, 74, 76, 72, 71, 75]
>>> print(np.mean(height_list)) # media73.1923076923077>>> print(np.median(height_list)) # mediana73.0>>> print(np.std(height_list)) # desviación estándar2.572326554954764>>> print(np.max(height_list)) # máximo79>>> print(np.min(height_list)) # mínimo69

Como puedes ver, hacer operaciones matemáticas es extremadamente sencillo y muy diferente a hacerlo con listas de Python. Además, en NumPy encontrarás muchas otras funcionalidades como trigonometría, logaritmos, valores absolutos, exponenciales, constantes universales, etc. Cualquier cosa matemática que necesites la encontrarás en su documentación.

Ejercicios de NumPy

Ahora que ya dominas los conceptos básicos, es hora de ponerlos en acción. Te dejaré una serie de ejercicios, resuélvelos con la ayuda de NumPy y deja tu código con sus resultados en los comentarios.

Para esto te he dejado en el notebook que te compartí al inicio una base de datos de jugadores de beisbol, la cual tiene 2 columnas principales: altura (pulgadas) y peso (libras). No te preocupes, en el notebook ya te las dejé listas como ndarrays con el nombre de height y weight. Esto es lo que tienes que hacer:

1. Crea un nuevo array en el que transformes las unidades de las alturas a metros (pista: multiplica por 0.0254).
2. Crea un nuevo array en el que transformes las unidades de los pesos a kilogramos (pista: multiplica por 0.453592).
3. Ahora vas a crear un nuevo array en el que calcules el IMC (Índice de Masa Corporal) de los jugadores a partir de los 2 vectores que creaste (pista: la fórmula es peso / altura²).
4. ¿Cuál es el máximo IMC? ¿Y el mínimo?
5. ¿Cuál es la media y la mediana del IMC? ¿Los valores son cercanos o hay un sesgo en los datos?
6. ¿Qué hay de la desviación estándar?
7. ¿Cuál es el peso y altura del jugador #734? ¿Es posible unificar los vectores en una matriz para obtener este resultado?
8. Esto último no lo vimos en el tutorial, así que será un reto para ti. Vas a intentar filtrar los datos para obtener cuántos jugadores tienen un IMC por debajo de 21 (pista: es posible hacerlo en una línea).

Despedida

¿Cómo te fue con los ejercicios? ¿Pudiste con todos? No te preocupes si fallaste en alguno, estaré ayudándote en los comentarios.

Recuerda que esta es una guía viva, así que si crees que faltó algo por explicar, déjalo en los comentarios y pronto lo añadiré. 😉

Por cierto, si estuviste siguiendo el notebook que te compartí, al final te dejé un par de sorpresas. 🎁

Aprende más de NumPy en el Curso Básico de Manipulación y Transformación de Datos con Pandas y NumPy

Además, te recomiendo seguir tu aprendizaje con el Curso de Fundamentos de Álgebra Lineal con Python. En este curso aplicarás todo lo que has aprendido de NumPy y aprenderás mucho sobre las funciones matemáticas de álgebra lineal, estoy seguro de que lo disfrutarás (spoiler: es uno de mis cursos favoritos en Platzi y aprenderás a resolver sistemas de ecuaciones con un par de líneas).

Y no solo eso, ¿recuerdas que te hablé sobre el broadcasting? En este curso entenderás todo sobre el tema.

Te había prometido un notebook, pero te mentí, te daré dos. Aquí tienes las notas que fui tomando del curso:

Apuntes del Curso de Fundamentos de Álgebra Lineal con Python en Platzi

Ahora sí, no tienes excusa para no iniciarlo. ¡Nunca pares de aprender! 💚