Resolución de Ecuaciones con Operaciones Combinadas
15/31Recursos
Problemas de álgebra para practicar.
Puedes usarlos siguientes problemas de álgebra para practicar los demás temas. Recuerda utilizar el correcto orden de despeje y las propiedades de las ecuaciones.
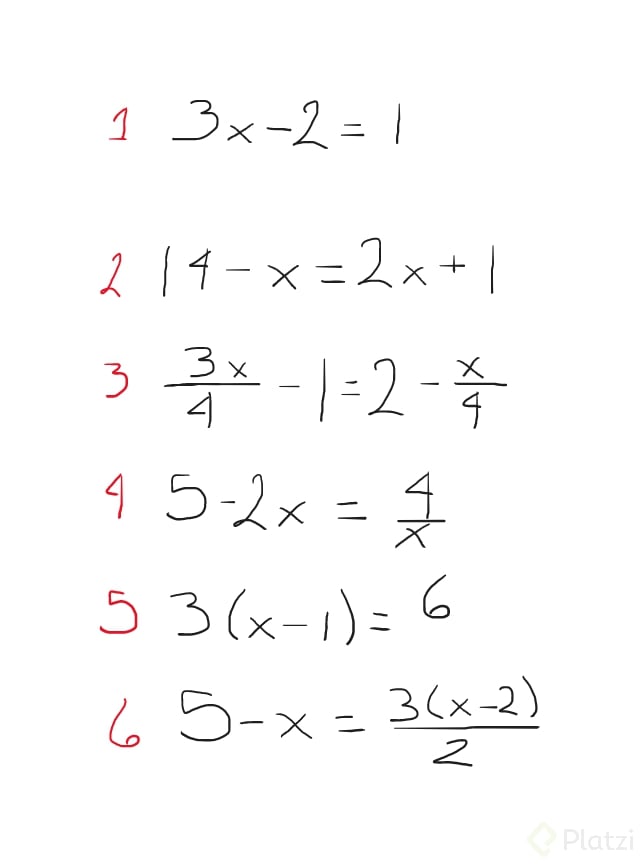
Contribución creada con aportes de: Mayra López.
Aportes 1442
Preguntas 63
Ordenar por:
Encontré esta opción online para escribir mi solución. La web te permite escribir ecuaciones, con los símbolos y demás! Por si a alguien le interesa:
http://www.wiris.com/es/solutions/htmleditor
Dado que la raíz cuadrada de 9 es 3 o -3, tenemos dos respuestas, una de ellas es 11/4 y la otra es -1/4
Lo subiría si mis números se entendieran pero, me dio x=11/4
A mi me dio x=11/4 y también x=-1/4
resuelto
Qué ejercicio tan genial. Hay dos resultados, ambos correctos.
X = -0,25 y también X=2,75.
Adjunto foto de prueba
-
3x-2=1
3x=1+2
3x=3
x=3/3
x=1 -
14-x=2x+1
-x-2x=1-14
-3x=-13
(-3x)/-3=-13/-3
x=-13/-3
x=13/3 -
(3x/4)-1=2-(x/4)
4((3x/4)-1)=4(2-(x/4))
3x-4=8-x
3x+x=8+4
4x=12
x=12/4
x=3 -
3(x-1)=6
3x-3=6
3x=6+3
3x=9
x=9/3
x=3 -
5-x=3(x-2)/2
5-x=3x-6/2
2(5-x)=2(3x-6/2)
10-2x=3x-6
-2x-3x=-6-10
-5x=-16
-5x/-5=-16/-5
x=16/5
((4x-5)/2)^2 = 9
Sacamos raíz a ambos lados de la ecuación
(4x-5)/2 = 3
Multiplicamos 2 a ambos lados
(4x-5)/2 * 2 =3 * 2
4x - 5 = 6
Sumamos 5 a ambos lados
4x - 5 + 5 = 6 +5
4x = 11
Dividimos 4 a ambos lados
4x/4 = 11/4
x = 11/4
Nos da que el resultado x = 11/4
Buen día mi resultado es X=11/4
Primero Aplicar Raiz de 2 en ambos lados de la ecuación
(4x-5)/2=3
Siguiente el 2 se multiplica en ambos lados, no se puede hacer la sustracción primero porque el 2 esta afectando a 4x y -5 por igual.
4X-5=3x2
Luego se suma en ambos lados +5
4X=6+5
Y finalmente se divide en ambos lados el 4
X=11/4
Hay dos soluciones:
X = 11/4, -1/4
Hay dos soluciones
x=11/4 y x=-1/4
si la raiz de 9 es 3, el valor de x = 11 / 4 y si el valor de 9 es -3, el valor de x = - 1/ 4
x= ±11/4
(4x-5/2)^2=9
4x-5/2=3 // Sacamos raíz en ambos lados
4x-5=6 // Multiplicamos 2 en cada lado
4x=11 // Sumamos 5 en cada lado
X=11/4 // Dividimos 4 en cada lado
Cual es del ordende operación en este caso? , no se parte por las sumas y restas ?
x1=11/4
x2=-1/4
Mi resultado fue x=11/4
x = (32+5)/4 = 11/4
x = (-32+5)/4 = -1/4
😃 ❤️
x1= 11/4
x2= -1/4
Gente les recuerdo que si tenemos en cuenta que (-3)(-3) tambien es = 9, la respuesta es tanto negativa como positiva, por eso el x subyasente 1 y 2
¿Cómo puedo subir mi ejemplo ?
Hola a todos, la primer respuesta que tuve al realizar este proceso fue errada,ya que no aplique la ley inversa del despeje, después de mirar las respuesta de todos caí en cuenta,
Mi respuesta final es 11/4
X1 = 11/4 X2 = -1/4
Hay dos respuestas porque la raíz cuadrada de 9 puede se 3 o -3.
( 4x - 5 / 2 ) ^ 2 = 9
step 1: √(4x - 5 / 2) ^2 = 9 --> (4x - 5/ 2) = √9
(4x - 5/ 2) ^ 2 = √9
step 2: (2(4x - 5)/ 2) = √9 * 2 --> 4x - 5 = 3 * 2
4x - 5 = 3 * 2
step 3: 4x - 5 + 5 = 6 + 5 --> 4x = 11
4x = 11
step 4: 4x/4 = 11/4 --> x = 11/4
Result: x = 11/4
😃
Solución 1: X= 11/4
Solución 2: X= -1/4
Lo despejé primero con la división, y me dio x=1.19; al ver los ejercicios de mis compañeros supe el error, debí despejar primero la potencia, , luego la división y ahí ya es más sencillo despejar lo demás. X= 11/4
Hola a todos.
Dejo mi ejercicio y una disculpa por la mala calidad de la foto.
Este es mi resultado 😃
Mi solución
x = 11/4
Mis resultados a los problemas encontrados en recursos son:
- x=1/3
- x=13/3
- x=3
- 5x-2x*2=4
- x=3
- x=16/5
serían 2 resultados para x= 11/4 y -1/4
Resultado =11/4
Aquí dejo mi solución, me dio dos valores por la raíz cuadrada de 9
Solución a la ecuación [(4x-5)/2]^2 = 9:
-Se obtiene raíz cuadrada de ambos lados:
√[(4x-5)/2]^2 = ±√9
(4x - 5)/2 = ±3
-Se multiplica por 2 ambos lados:
(4x - 5)/2 (2)= ±3 (2)
4x-5 = ±6
-Se suma 5 de ambos lados:
4x-5+5 = ±6+5
4x_1 = 11 & 4x_2 = -1
-Se divide entre 4 ambos lados:
4x_1 (1/4) = 11(1/4) & 4x_2 (1/4)= -1 (1/4)
x_1 = 11/4 & x_2 =-1/4
Luego de esos ejercicios anteriores este reto no es nada!
Aquí les dejo mi reto en Notion (es el último) junto con los anteriores ejercicios 😃
Mi respuesta es x=11/4
Gracias a todos por sus aportes logré comprender las dos respuestas.
Una herramienta muy interesante cuando no entendemos un ejercicio es PhotoMath, ya que no sólo nos dice la respuesta, pero nos muestra el paso a paso de la resolución, con lo que podemos ir entendiendo cómo llegar al resultado y luego seguir resolviendo ejercicios nosotros mismos.
https://photomath.com/
Desarrollo:
((4x-5)/2)^2 = 9
Elevamos a la potencia 2 en ambos lados de la ecuación
[((4x-5)/2)^2]^1/2 = (9)^1/2
(4x-5)/2 = 3
Multiplicar por 2 en ambos lados de la ecuación
((4x-5)/2)2 = 32
4x-5 = 6
Sumar 5 en ambos lados de la ecuación
4x-5 +5 = 6 +5
4x = 11
Dividimos por 4 en ambos lados de la ecuación
4x/4 = 11/4
x = 11/4
Me dio
x=11/4
mi resultado:
Xi= 11/4 Xii= -1/4
Les comparto mi proceso. Se darán cuenta que en mi primer intento cometí un error puesto que no tuve en cuenta que todo estaba dentro de paréntesis, por lo que comencé con la división que veía ahí. Luego de corregir eso pude llegar satisfactoriamente a los resultados correctos. Espero que esto sirva de guía, no se desanimen si no les sale a la primera, descubran sus errores, corríjanlos y sigan adelante.
SOLUCION
((4x-5)/2)^2 =9
raiz(((4x-5)/2)^2 ) = raiz(9)
((4x-5)/2) = 3
2*((4x-5)/2) = 23
4x-5 = 23
4x-5 = 6
4x-5 +5= 6+5
4x= 11
x=11/4
Lo resolví paso a paso y lo grabe. Espero les ayude.
https://youtu.be/NR-_P2DYSqI
X1 = 11/4
X2 = -1/4
Sólo me queda la duda que si hubiese despejado primero la resta, luego multiplicación, división, etc, me daría un valor diferente.
Saludos!
Tuve un pequeño problema con la raíz pero después de revisar mi resultado fue x = 11 / 4 y también debido a que la raíz cuadrada de 9 puede ser 3 o -3 mi segundo resultado fue x = -1 / 4
X= 11/4
X=11/4
2.75
Esta es mi respuesta:
Esta bien hecho. Luego de fallar con el orden, multiplique 2 a lo ultimo de todo, era multiplicar luego de sacar la raíz cuadrada de 9 e seguir con lo otro.
x1 = 11/4
x2 = -1/4
Me salió x=11/4 , tengo ganas de un reto más ambicioso jeje
X = 11/4
Que satisfacción la de entender completamente todo lo que ves! Gracias
11/4
11/4
X = 11/4
x= 11/4
X = 11/4
En el fondo es genial resolver esto, creo que la matemática entre otras cosas ayuda a crear confianza en uno mismo y a lo mejor ese es uno de los principales trabajos de los profesores de secundaria con matemática.
Excelente Sergio, gracias por las explicaciones.
He hecho una generalización del ejercicio, formando una especie de modelo para resolver las ecuaciones de este tipo:
De momento la plataforma no me deja subir la imagen , pero mi resultado es x= 11/4
√9=3
3x2 =6
6+5 =11
11/4 = 2,75
La respuesta es x=±11/4
11/4
11/4
x1=11/4 o x2=-1/4
Muy buenas explicaciones Sergio.
Solucion:
x= 11/4
x= -1/4
x = 11/4 , x = 2.75
Lo hice y me dio x=11/4. Después de pasarlo por Mathway me daba como respuesta también -1/4. No entendía porque hasta que recordé que la raíz de 9 puede ser 3 o -3.
X = 11/4
X1=11/4
X2= -1/4
hay dos posibles soluciones:
- 11/4
- -1/4
11/4
x = 11/4
ó
x = -1/4
La respuesta es 11/4
Esta es la solución del reto:
X = 11 / 4
x=11/4 o x=-1/4
¿Quieres ver más aportes, preguntas y respuestas de la comunidad?