Para hallar el valor de la pendiente conociendo dos puntos de la recta se usa la siguiente fórmula:
Pero… ¿qué significa esta fórmula?
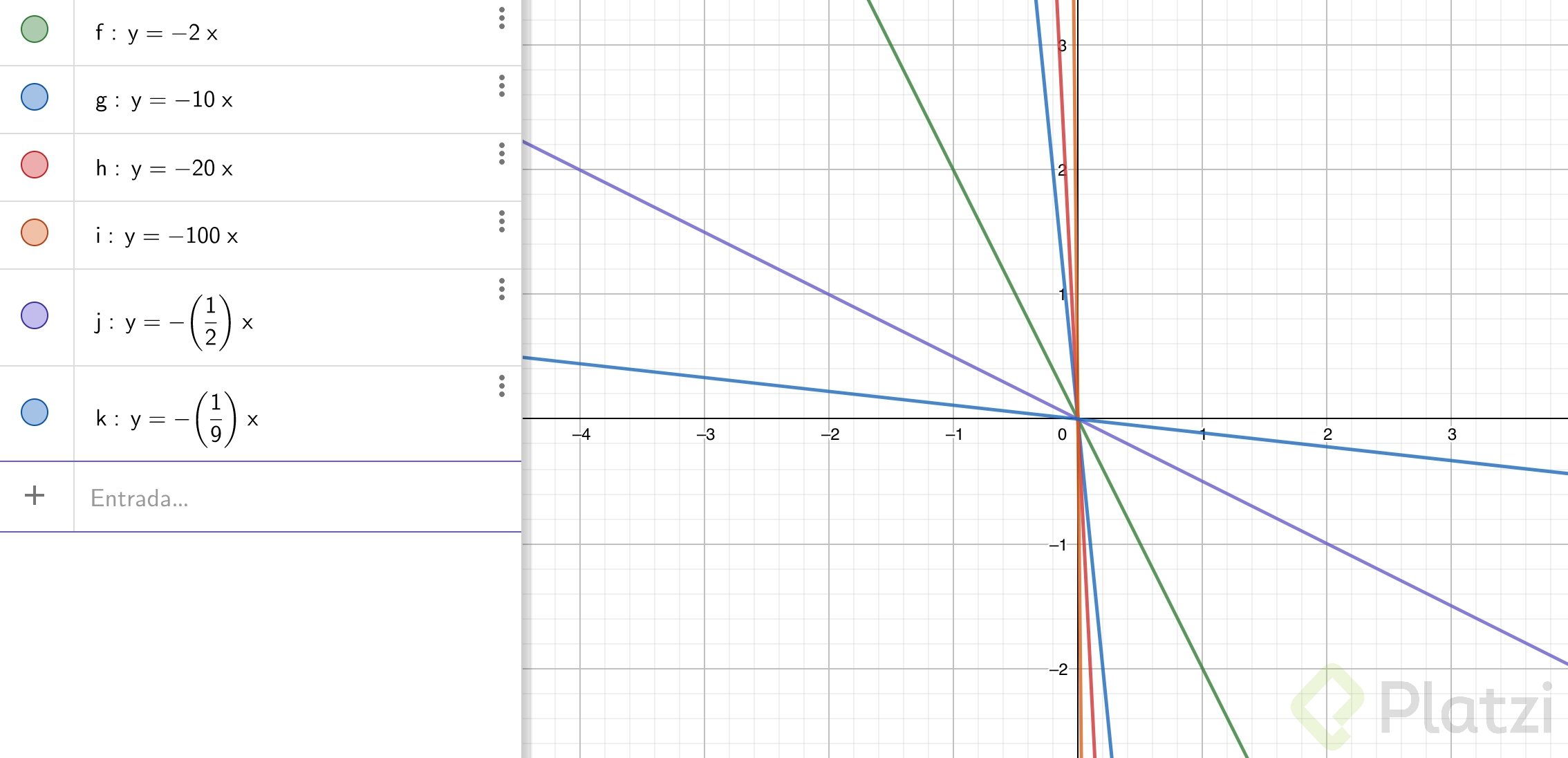
Como lo explicó el profesor, la pendiente me indica cuánto va ha variar un valor con respecto a otro: Mientras mayor sea la pendiente, mayor será su variación.
Primero veamos cómo se relacionan los ejes o qué significan los ejes:
El eje de la abscisas (eje x) nos indica en qué “momento” de la gráfica estamos, mientras que el eje de las ordenadas (eje y) nos indica el valor de la función en dicho momento (valor de x).
Por lo tanto, hallando cuánto varía el valor de la función con respecto a los momentos en los que analizamos la función, estaremos hallando la pendiente.
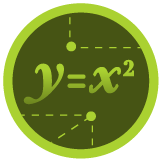













































![Francisco Garcia [C6]](https://static.platzi.com/media/avatars/avatars/garciafran_c845c2fe-2ea4-42db-a305-a7f4ef13b0fd.jpeg)
































¿Quieres ver más aportes, preguntas y respuestas de la comunidad?