En el último ejemplo 6ax + 3a + 1 + 2x el resultado es ( 2x + 1 )( 3a + 1)
Conceptos Básicos
Conceptos Básicos de Álgebra: Variables y Constantes
Leyes de los Signos en Operaciones Aritméticas y Algebraicas
Signos de Agrupación: Uso y Jerarquía en Operaciones Matemáticas
Leyes Básicas de Exponentes y Aplicaciones Prácticas
Leyes de Exponentes: Potencia de Potencia y Radicación
Reglas del Lenguaje Algebraico: Expresiones y Operaciones Básicas
Álgebra Básica: Ejercicios y Conceptos Fundamentales
Operaciones entre polimonios
Suma y Resta de Polinomios: Ejemplos Prácticos
Operaciones entre monomios
Multiplicación de Monomios: Reglas y Ejemplos Prácticos
División de Monomios: Ley de Exponentes y Ejemplos Prácticos
Productos Notables
Binomios al Cuadrado: Regla y Ejemplos Prácticos
Binomio al cuadrado: fórmula y ejemplos prácticos
Elevación de Binomios usando el Triángulo de Pascal
Binomios Conjugados: Cálculo y Aplicaciones Prácticas
Propiedades del Binomio al Cubo y Diferencia de Potencias
Factorización
Factorización por Factor Común Monomio: Ejemplos Prácticos
Factorización por Agrupación de Términos Comunes
Factorización de trinomios cuadrados perfectos
Factorización de Diferencia de Cuadrados Perfectos
Factorización de trinomios cuadrados perfectos por adición y sustracción
Factorización de Trinomios de la Forma x² + bx + c
Ejercicios básicos de factorización algebraica
Ecuaciones
Ecuaciones: Conceptos Básicos y Resolución
Ecuaciones de Primer Grado: Transposición y Resolución
Resolución de problemas con ecuaciones lineales básicas
Métodos para Resolver Sistemas de Ecuaciones Lineales
Métodos de Igualación y Eliminación en Sistemas de Ecuaciones
Resolución de Ecuaciones Cuadráticas: Uso del Discriminante
Resolución de Ecuaciones Cuadráticas: Fórmula General y Factorización
Ecuaciones cuadráticas incompletas: caso ax² = 0
Resolución de Ecuaciones Cuadráticas Incompletas
Ecuaciones completas: definición y ejemplos
Contenido bonus
Solución de Sistemas de Ecuaciones con Fracciones
No tienes acceso a esta clase
¡Continúa aprendiendo! Únete y comienza a potenciar tu carrera
Si ya tienes una cuenta,
Factorización por Agrupación de Términos Comunes
17/33Recursos
Cuando nuestro polinomio presenta un factor común polinomio es cuento usamos esta forma de factorización.
Factorización por término común polinomio
- Para factorizar primero debes saber identificar cómo vas a formar los factores. Aquí tratamos de conseguir dos factores o más en los que al multiplicarlos, obtenemos la expresión original.
- Se comienza haciendo un paso parecido al anterior caso, y es el de buscar qué factor común se puede sacar de un grupo de expresiones.
- Es buena idea comenzar buscando las constantes que sean iguales en un grupo de expresiones para sacarlas como factor.
- Es importante que te fijes en los signos, ya que dependiendo de cómo estén organizados en la expresión original, van a cambiar su orden en su equivalente factorizado.
- La factorización hace lo contrario a los productos notables.
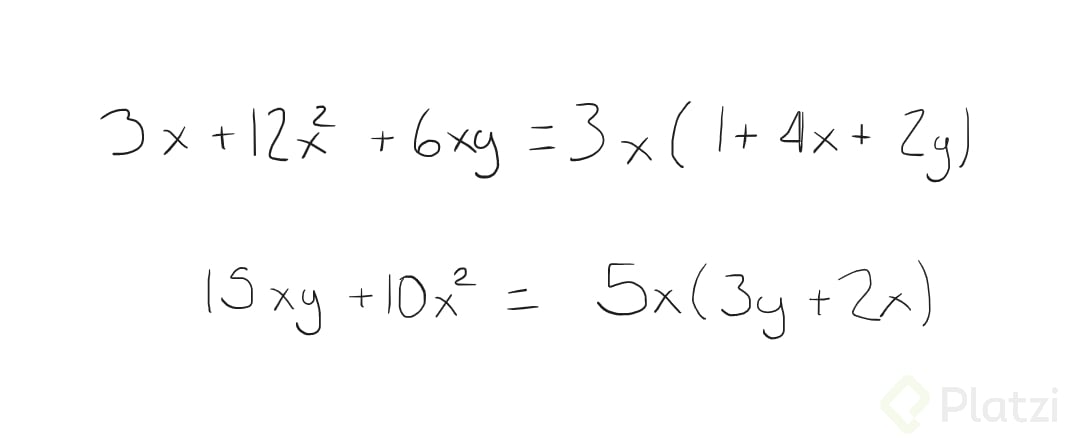
Contribución creada con los aportes de: Mayra López.
Aportes 81
Preguntas 14
Ordenar por:
Nunca deja nada en los archivos
Al final colocaste (2x-1)(3a+1) y es (2x+1)(3a+1), pero de igual forma muy buena clase
Para evitar confusiones, si, en el último ejemplo la respuesta es realmente (2x+1)(3a+1).
Por otro lado, creo que esto muestra que ya será más que nos eduquemos a ver estos patrones para poder ver las posibilidades de factorización en cada caso. Hacer ejercicios para tomar agilidad es lo que necesitaremos después de clases tan claras como esta.
Si hubiera aprendido así, no me hubiera dado tanto dolor de cabeza.
El curso esta muy genial, pero salta de la clase de multiplicación a Factor común por agrupación de términos.
Concepto fundamental: La factorización es el procedimiento algebraico contrario al de los productos notables, es decir los binomios.
La respuesta del último ejercicio xd.
.
La clase esta mal ordenado 😦
Es buena idea comenzar buscando las constantes que sean iguales en un grupo de expresiones para sacarlas como factor
Al final del video no corresponde a 2x-1 sino a 2x+1, verdad?
Me sorprende mucho como utilizamos propiedades de la multiplicacion y división de clases pasadas, mientras en el colegio te dicen ""así se hace por que si"
Excelente! Como recomendación los archivos deberian estar colgados justo cuando terminen las clases, para asi hace mas facil la practica.
la verdad la maestra no explica tan bien 😦
Este método de factorización sirve para expresiones con 4 o 6 términos. Y debe usarse solo en caso de que no podamos encontrar un factor común a todos los términos.
- Observamos el polinomio y vemos qué grupos podemos formar según los factores comunes.
- Debemos formar 2 grupos (aprovechando que los términos son conmutativos, se pueden cambiar de orden).
- Factorizamos esos 2 grupos y debemos buscar que de ambas factorizaciones obtengamos el mismo paréntesis.
- Este mismo paréntesis nos servirá para factorizar
explicación clara aunque con un pequeño bug en el minuto 11:07 en la explicación menciona 2x+1 (lo correcto) y en la practica escribe 2x-1 (incorrecto)
Explicación muy clara, solo que en la parte final del último ejercicio se hace la agrupación del (2x-1) cuando en realidad es (2x + 1).
Un ejemplo adicional 😄:
Excelente explicación. Hay un error de escritura en el ultimo ejemplo, pero en el desarrollo verbal esta bien, fue solo un despiste de escritura. Excelente clase.
En el minuto 11:06 coloca la expresión (2X-1) siendo lo correcto (2X+1), pero ella dice que es positivo, es solo un error de escritura. De resto todo bien. Muy buena clase. Elegante!
es mejor factorizar paso a paso para que los signos nos que queden bien organizados
el producto notable es la operacion inversa de la factorizacion.
me gusto la explicacion
Super claro
Sigo recordando esto de factorizacion y la verdad si es disfrutable.
El factor común por agrupación de términos es una técnica de factorización que se utiliza cuando una expresión algebraica tiene más de dos términos y no es evidente un factor común monomio en todos los términos. En lugar de eso, los términos pueden agruparse de manera que se encuentre un factor común en cada grupo, y luego se extrae este factor común.
Les dejo más ejercicios para que practiquen. Las respuestas están abajo.
\----
**Respuestas**
Existe un error en el último ejercicio explicado.
Sin embargo, buena explicación.
siento que da mucho y no se ponen ejercicios deberían ser por lo menos 20 por video, no me gusta solo tener 5 ejercicios de cada tema… y además ir buscando cual es la parte del curso que tiene los 5 ejercicios
Nota :El factor común se puede ver como el inverso de la propiedad distributiva.
Ya que si tenemos: 6ax+3a luego de aplicar el factor común nos queda 3a(2x+1) podemos aplicar la propiedad distributiva para volver a como teníamos el ejercicio al principio.
Si quieren ejercicios les dejo el siguiente enlace. Vienen con respuestas para que puedan verificar.
https://matematicasn.blogspot.com/2015/12/factorizacion-por-agrupacion-de.html?m=1
Ese primer paso, de hacer factor común de los monomios, es importante para evitar confusiones
El ultimo ejemplo me confundió un poco, entiendo que la respuesta es correcta, solo me cuesta trabajo tener esa intuición para identificar cuando se puede realizar esa simplificación. En fin, solo queda practicar. ❤️
Un consejo que me acaba de pasar si no recuerdan el porque de algo sigan viendo el vídeo, transcriban en físico y luego al estar mas avanzado volver al inicio y seguro saldrán de dudas.
Me encantó la explicación, salvo por el error pero olvidando eso todo bien 😃
Que bueno que otros ya han comentado sobre la equivocación del siglo menos en el íltimo ejercicio, pensé que era alguna inversión de signo al reescribir la cantidad. ja ja ja, suele pasar.
Muchas gracias.
🤔🤔🤔
Concepto fundamental: “La factorización hace lo contrario a los productos notables.”
No me lo dijeron de esa manera, muy bueno
Para todos aquellos que consideren insuficiente el desarrollo o el tipo de explicación de estas clases, recomiendo profundamente el canal de Youtube de Matematicas del profe Alex.
<https://www.youtube.com/@MatematicasprofeAlex>
En general solo buscando por el título del tema, aparece una clase que considero que tiene una calidad mejor y sirve como complemento a estos materiales de Platzi!
El último ejercicio me ha volado la cabeza, hoy si he aprendido cosas nuevas.
En el minuto 11:24, el factor es (2x+1) y no (2x-1)
La factorización es lo contrario a los productos notables.
La factorización por término común polinomio consiste en buscar factores cuyo producto sea igual a la expresión original. Se inicia identificando un factor común en un grupo de expresiones, preferiblemente constantes iguales, y se debe tener cuidado con los signos, ya que pueden cambiar su orden al factorizar. Este proceso es el opuesto a los productos notables.
4a³b - 2ab + 6ab²: El factor común aquí es 2ab. Al sacarlo como factor, el polinomio factorizado es 2ab(2a² - 1 + 3b).
Equipo Platzi, por favor deberían cargar los ejercicios en la sección de recursos, la profe viene motivando a hacerlos pero no están cargados
17. Factor común por agrupación de términos
Factor común polinomio
Conseguir dos factores que al hacer su producto nos dé como resultado lo anterior
La factorización es lo contrario a los productos notables
Malisima explicando, rehagan el curso con alguien que sepa explicar.
ax + bx + ay + by
x(a+b)+y(a+b)
(x+y)(a+b)
am-bm+an-bn
m(a-b)+n(a-b)
(m+n)(a-b)
6ax + 3a + 1 + 2x
3a(2x+1)+1(1+2x)
(3a+1)(2x+1)
Muy buena la explicación 😃
Fue demasiado directo, pero estuvo buena la clase
la respuesta del ultimo ejercicio no seria (2x+1)(3a+1) por que la profesora puso ¨(2x-1)
En el ultimo ejemplo, el 1 no lo escribimos cuando factorizamos, pero cuando juntamos las 2 expresiones, si lo tenemos en cuenta, es decir ese 1 nunca se puede omitir?
Tercer ejemplo 6ax + 3a + 1 + 2x
Segundo ejemplo
Primer ejemplo ax + bx + ay + by
Algebra de Baldor capitulo 7 , todo sobre factorización
Buena explicación.
puso menos en vez de mas
#El material está mal ordenado, y salta de la clase de multiplicación hasta ésta
Algunos ejercicios mas aqui.
https://es.khanacademy.org/math/algebra-home/alg-polynomials
Nunca entendí bien esta forma de factorización, finalmente ya me quedo claro.
Sencillo
Muy buenos ejemplos, Marce!
Super claro.
Excelente clase.
Entendido!
No entendi
Esto está genial.
bien
El último ejercicio, el resultado corregido es: (2x+1)(3a+1).
La factorización en este último ejercicio en realidad sería: (2x+1)(3a+1)
En la escuela no entendi como hacerlo, pero ya lo entendi! Gracias!! 😃
¿Quieres ver más aportes, preguntas y respuestas de la comunidad?